一题多变05——三角形内点问题

原题 如图1，P是等边三角形ABC内的一点，连结PA，PB，PC，若PA：PB：PC＝3：4：5，求∠APB的度数.

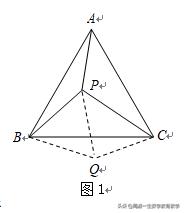
分析：欲求∠APB的度数，考虑到PA：PB：PC＝3：4：5，联想到勾股定理的逆定理，以PA、PB、PC为边的三角形是直角三角形，因此，设法将PA、PB、PC变换到同个三角形中.注意到△BAP的边BA与BC“共点等长”，根据经验对△BAP实施旋转变换。

解：因为△ABC是等边三角形，

所以BA=BC，∠ABC=60°，

所以将△BAP绕点B顺时针旋转60°，可得△BCQ，

连结PQ.设PA＝3a，则PB＝4a，PC＝5a，

由旋转不变性，得

QB＝PB=4a，QC =PA =3a，∠PBQ＝60°，

所以△PBQ是等边三角形，

所以PQ＝PB＝4a，∠PQB＝60°，

在△PQC中，

因为PQ^2+QC^2=16a^2+9a^2=25a^2=PC^2,

所以△PQC是直角三角形，∠PQC＝90°，

所以∠BQC＝90°+60°=150°，

所以∠APB＝∠BQC＝150°。

变式一：如图2，已知P是等边△ABC内一点，∠APB＝150°，求证：PA^2+PB^2=PC^2.

（提示：将△BAP绕点B旋转60°,可得△BCQ）

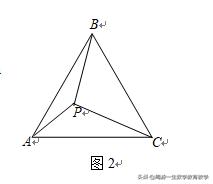
变式二：如图2，已知点P是等腰直角△ABC内一点，AB＝AC，∠BAC＝90°，PA＝1，PB＝√2，PC＝2，求∠APB的度数.

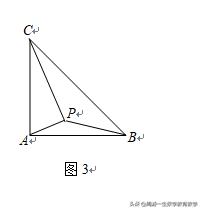
（答案：135°）

变式三：如图4，P、Q是等腰Rt△ABC斜边AB上两点，且∠PCQ＝45°，求证：AP^2+BQ^2=PQ^2.

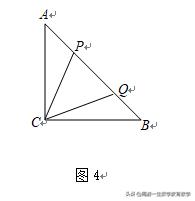
(提示：将△ACP绕点C顺时针旋转90°)