经典再现19——正方形问题：E是正方形ABCD外一点，满足BE=BD

题：如图，已知E是正方形ABCD外一点，满足BE=BD，CE∥BD，BE交CD于F，

求证：DE=DF.

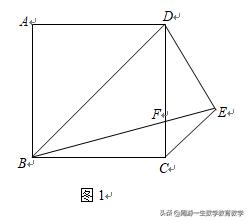
分析：欲证DE=DF，设法证明∠DEF=∠DFE.

从已知出发，根据已知条件联想到其相关的性质。

由四边形ABCD是正方形，可得该四边形四边相等，四个角都是直角，对角线与边的夹角为45°；

由BE=BD，可得∠BED=∠BDE；

由CE∥BD，可得∠BEC=∠DBE，∠DCE=∠BDC=45°.

经过探索，以上这些条件仍然不足以证明∠DEF=∠DFE.

考虑添加辅助线.注意到正方形对角线互相垂直评分且相等，为了利用这个性质，连接AC，交BD于点O（如图2）.则

AC⊥BD，OC=BD/2.

因为CE∥BD，所以AC⊥CE，

从而有∠DOC=∠OCE=90°.

考虑到这两个直角，再作EG⊥BD于G（如图2），

则四边形OCEG是矩形，

所以EG=OC=BD/2.

注意到直角三角形BGE中，

因为BE=BD，所以EG=BE/2，

所以∠EBG=30°.

这是个伟大的发现，发现了∠EBG为30°，接下来的问题就不成问题了.

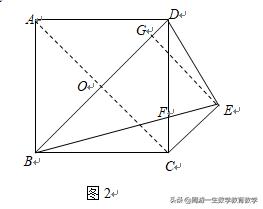
证明：连接AC，交BD于点O（如图2）.则

AC⊥BD，OC=BD/2.

因为CE∥BD，所以AC⊥CE，

作EG⊥BD于G（如图2），

则四边形OCEG是矩形，

所以EG=OC=BD/2.

在直角ΔBGE中，

因为BE=BD，

所以EG=BE/2，

所以∠EBG=30°，

所以∠BDE=∠BED

=(180°-30°）/2=75°，

因为∠BDC=45°，

所以∠EDF=30°，

所以∠DFE=180°-30°-75°=75°，

所以∠DFE=∠DEF，

所以DE=DF.