课本给出了三种求解一元二次的方法：配方法、公式法和因式分解法。比较一下这三种方法，我们发现背后都有一条的主线，那就是“降次”。

什么是降次

这里的“次”，指的是方程中未知数的次数。降次，就是降低方程中未知数的次数，确切点说，是降低方程中未知数的最高次数。

比如以下方程：

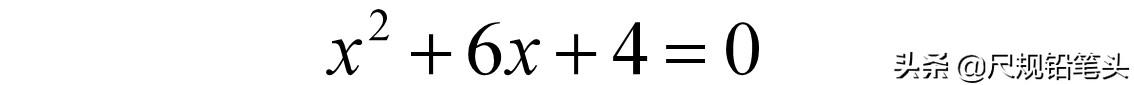
方程的左边有3个单项式，它们的未知数次数分别是2次、1次和0次，最高次数在第1项，为2次。降次就是要把这里最高的2次降到1次。

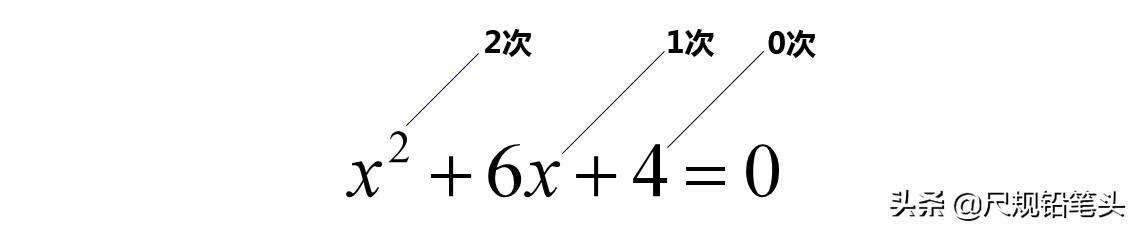
降次后，一元二次方程的求解就转化为一元一次方程的求解了。这也是进行降次的目的。

很多时候，新知识的出现都是为了帮助我们把复杂的问题转化为简单问题进行处理。

一元二次方程的求解思路

还没学习一元二次方程之前，如果你拿到上述的方程1，你会怎么去求解呢？

1、类比法探究解题思路

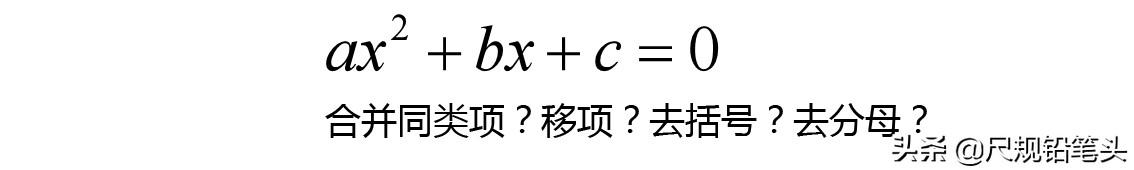
因为我们已经学过一元一次方程，所以我们首先想到的就是对比一下两种方程的差别，看看能不能借鉴一元一次方程的求解方法。求解一元一次方程时，我们运用了四个基本方法：合并同类项、移项、去括号和去分母。但是无论哪个方法都无法改变二次项的次数。因此，我们必须先解决二次项的问题。

2、逆向思维探究解题思路

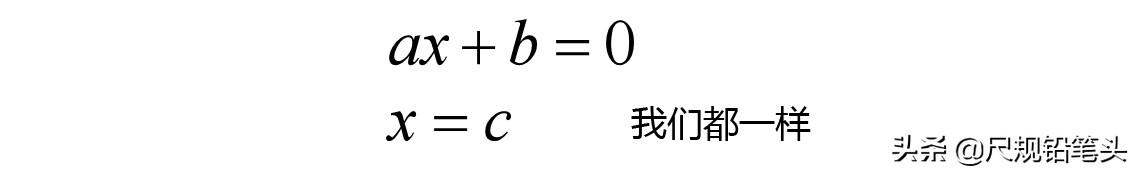
运用逆向思维，我们先观察一下方程解的形式。不难发现，方程的解也是一个一元一次方程，只是它的形式比较特别：方程的左边有且只有一次项未知数，并且系数为1，而方程的右边没有未知数。如果解决了二次项的降次问题，一元二次方程的求解就转化成了一元一次方程的求解。

3、确定二次项降次方法

方法A

二次项降次为一次项，最基本的方法就是开方。前提是，除含未知数的完全平方式以外，不能含有未知数，否则开方后可能出现含未知数的无理数，与我们解方程的初衷越来越远。

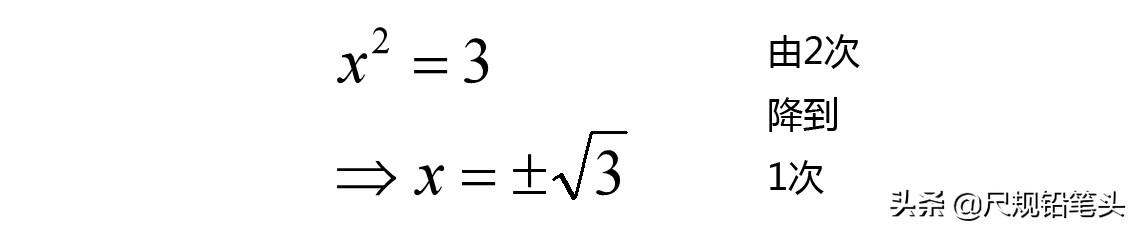
方法B

根据定义，二次方等于两个一次方相乘，因此我们可以考虑把二次多项式分解成两个一次多项式的积，同时考虑到方程的右边为0，只要保证每个一次多项式为0，方程就成立。

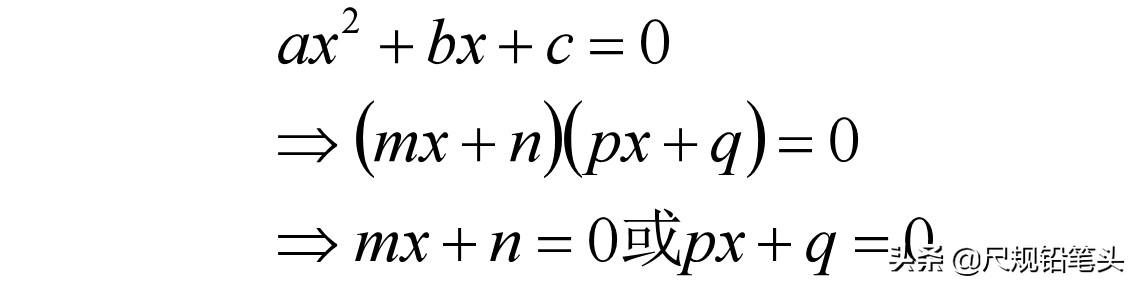
由上，无论是方法A还是方法B，求解一元二次方程，都可以先把一元二次方程转化为一元一次方程，然后再调整一元一次方程的形式，从而得解。

降次如何在三种解法中体现

1、配方法

从二次转化成一次，最基本的方法就是开方。

对于只有二次项，没有一次项的一元二次方程，求解的方法非常简单，只需要移项再开方即可。

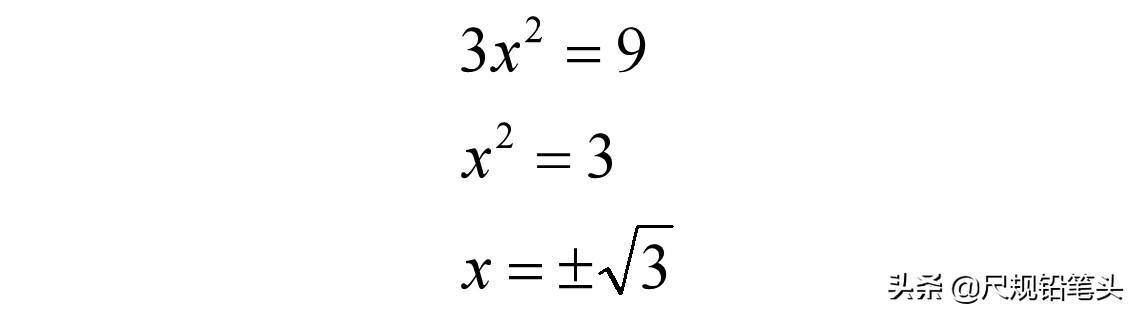
对于既有二次项也有一次项的一元二次方程，怎么办呢？这里就用到了完全平方和（差）公式，把原方程转化为只有二次项的形式，这样就又可以通过开方来求解了。

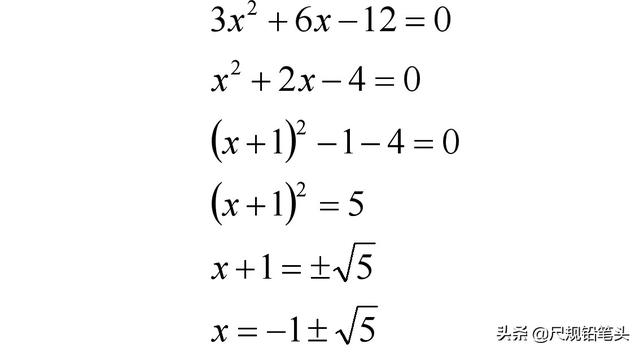
一般地，通过完全平方公式，把一次项和二次项全部装配到完全平方式中，从而通过开方降次求解方程，这就是配方法的由来。

2、公式法

公式法其实就是把配方法用公式表达出来而已，本质上就是配方法，所以求解的思路也是降次。

3、因式分解法

因式分解是为了降次，所以分解后的因式最高次数必须是一次。因式分解时，无论是提取公因式法还是公式法，最终目标都是分解二次项。

实际上，因式分解时最常用的方法是十字相乘法。

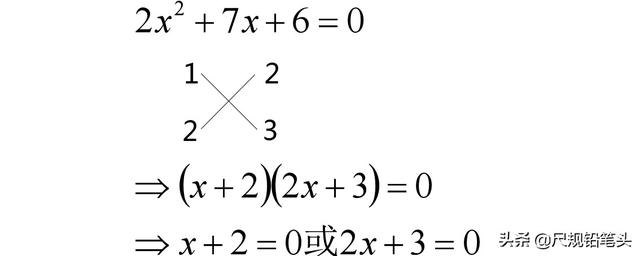
从上例可以看出，十字左边就是未知数的一次项，所以十字相乘法本身就隐含着降次操作。

善用降次思想解方程

由上面的分析，我们可以清楚地看到，一元二次方程的求解过程就是未知数降次的过程。

实际上，不但一元二次方程的求解主线是降次，以后我们要学到的多次方程的求解，也是以降次为主线的。不管是为了现在的学习还是为以后做准备，希望大家无论是看书还是做题的时候，都要细细体会其中的降次思想。