等腰三角形“经典例题”讲解

等腰三角形性质1、两边相等，两个底角也相等；简称“等边对等角”，反过来也是成立的简称“等角对等边”。

等腰三角形性质2、“三线合一”定理：既顶角角平分线、底边上的中线、底边上的高线重合为一条线。换而言之，等腰三角形中，你看到的顶角角平分线也就是它底边上的中线、或者底边上的高线。

下面我们来看看例题中的应用：

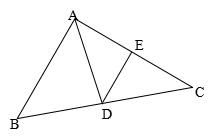
例1．如图所示，已知AD=DE=CE=BE，∠B=54°，求∠A的度数。

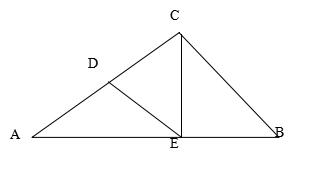
分析：本题重点是发现图中有几个等腰三角形，然后利用性质1来解答

比如：由AD=DE可推出∠A=∠DEA

由DE=CE可推出∠EDC=∠ECA

由BE=CE可推出∠B=∠ECB=54°

难点：发现∠EDC=∠A+∠DEA，（三角形的外角等与它不相连的两内角之和）

过程：

因为DE=CE所以∠EDC=∠ECA

因为AD=DE所以∠A=∠DEA=X

因为∠EDC=∠A+∠DEA=x+x=2X =∠ECA

因为BE=CE所以∠B=∠ECB=54°

所以在△ABC中可得：∠A+∠B+∠ACB=180

X+45+2X=180

3X=135

X=45

所以：∠A=45°

例2：如图，已知AB=2AC，∠1=∠2，DA=DB，则DC⊥AC，请说明理由。

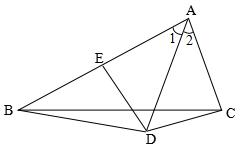
分析：本题中没有提到DE这条线，这显然是一条辅助线。做法是过点D做DE⊥AB，交AB与点E，然后通过证明△ADE与△ADC全等，从而得出∠ACD=∠AED，因为∠AED=90°所以∠AED=90°从而DC⊥AC。

过程：

过点D做DE⊥AB，交AB与点E

因为DA=DB所以AE=BE=1/2AB(三线合一）；

因为AB=2AC所以AE=AC

在△ADE与△ADC中

...

【小试牛刀】

1、等腰三角形的一边长为2cm，另一边长为4cm，则周长为 。

2、等腰三角形有的一个角为100°，则另两个角为 。

3、等腰三角形的一个角是另一个角的2倍，则这个三角形的三个内角的度数分别为 。

4、等腰三角形的底边长为4cm，则腰长的取值范围是

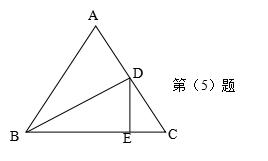
5、如图所示，△ABC中，AB=AC，BD是角平分线，BE=BD，∠A=72°，则∠DEC= 。

6、在“线段、角、三角形、等腰三角形、直角三角形、等边三角形”这些图形中，轴对称图形是 ；其中对称轴最多的图形是 ，它共有 条对称轴。

7、等腰三角形一个顶角与一个底角的和为110°，则顶角为 。

8、等腰三角形一腰上的高与底边的夹角为40°，则顶角的度数为 。

9、如图所示,在△ADC中，DE垂直平分AC，AE=3cm，△ABD的周长为13cm，求△ABC的周长。

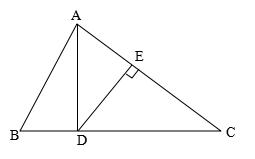
10．如图所示，在△ABC中，AD平分∠BAC，DE垂直平分AC，交AC于点E，交BC于点D，已知∠C=36°，求∠B的度数。