「中考复习」圆与相似综合题，设参表示相关线段是关键

在中考试题里，有一类求线段的比值，或求线段长度的题目，在模拟复习期间，许多同学们感到非常困感，找不到方法，为此有必要讲解一下此类题的常见解法，助力同学们中考时轻松破解此类题目。

【题目呈现】

☞1.如图，PA是⊙O的切线，A是切点，AC是直径，AB是弦，连接PB、PC，PC交AB于点E，且PA=PB.

(1)求证:PB是⊙O的切线;

(2)若∠APC=3∠BPC，求PE/CE的值.

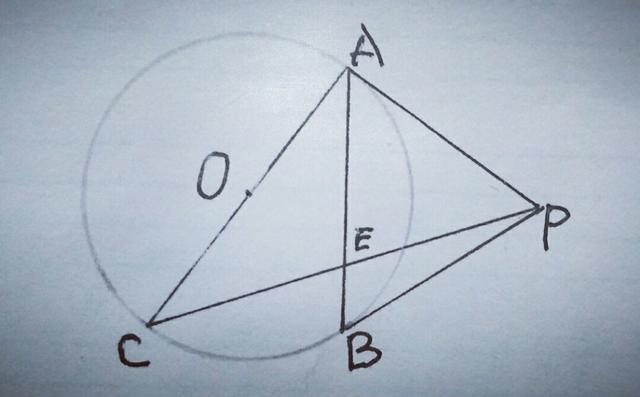
【分析】(1)较易，可连接OP，OB，如图:

证△OAP≌△OBP，得∠OBP=∠OAP=90°，从而得证.也可，利用OA=OB，PA=PB，推得∠OBP=∠OAP=90°，得证.

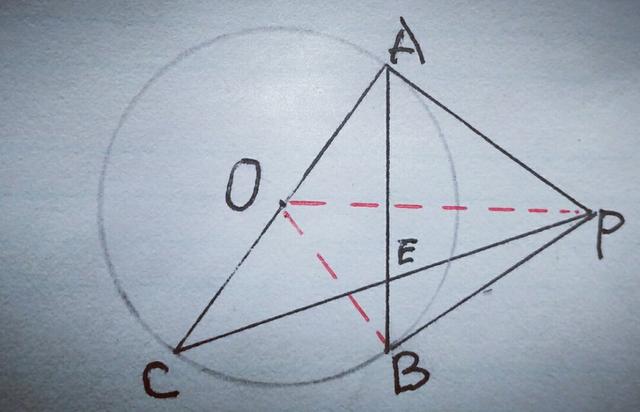
(2)同学们看见∠APC=3∠BPC这一条件感到困惑，与求PE/CE的值没有办法联系，求比值问题一般与相似进行联系，而条件中又没有给出一个比值，用相似等量代换的方法又行不通，感觉"山重水复疑无路"，这时，我们不妨回归条件，仔细分析题目，寻找问题的突破口，看第(1)问的结论，能否得到某些有用的信息等，需要深入联想，联想书中的有关定理，联想平时记忆的相关数学模型，这一过程正是同学们的薄弱环节，是学习数学的难点，数学难，难就难在这儿，这一过程突破了，学习数学也就不会太难了。我们平时要强化这一过程的训练，让思考成为一种习惯，提高驾驭数学知识的能力。就本题而言，PA，PB都是⊙O的切线，P为⊙O外一点，想到切线长定理，则∠APO=∠BPO，与条件∠APC=3∠BPC联系在一起，得出∠BPC=∠OPC，同时知道OP⊥AB，设F为垂足，由于AB为⊙O的直径，连接CB，则∠ABC=90°，∴OP∥BC，可知△PEF∽△CEB，从而PE/CE=PF/BC，如图:

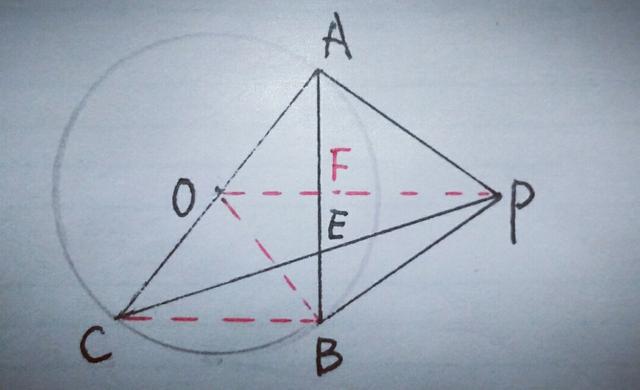
接下来只须求PF/BC即可，这时又遇到了问题，但我们心中明白，这样思考十有八九思考方向是正确的，那么PF与BC又如何联系数量关系呢？一鼓作气，趁兴追击，由上面的分析知BC=BP，F是AB的中点，OF是三角形ABC的中位线，BC=2OF，BP=2OF，在Rt△OBP中，直角边BP与OF有了关系，我们想到了射影定理的模型，可知BP²=OP×PF，为了更简单化一些，设OF=t，则BC=BP=2t，则(2t)²=PF(t+PF)，解得PF=(一1十√17)t/2(取正值)，这样通过设参数t，列方程，成功地表示出线段PF，∴PE/CE=PF/BC=(√17一1)/4.【设参，一方面为了简单，减轻大脑的负单，另一方面，为表示相关的线段】.

2.如图，在△ABC中，AB=AC，以AB为直径作圆O，分别交BC于点D，交CA的延长线于点E，过点D作DH⊥AC于点H，连接DE交线段OA于点F.

(1)求证:DH是圆O的切线;

(2)若A为EH的中点，求EF/FD的值;

(3)若EA=EF=1，求圆O的半径.

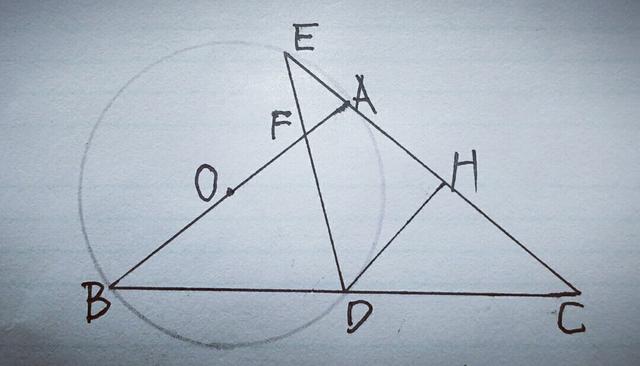
【分析】(1)较易，连接OD，AD，如图.

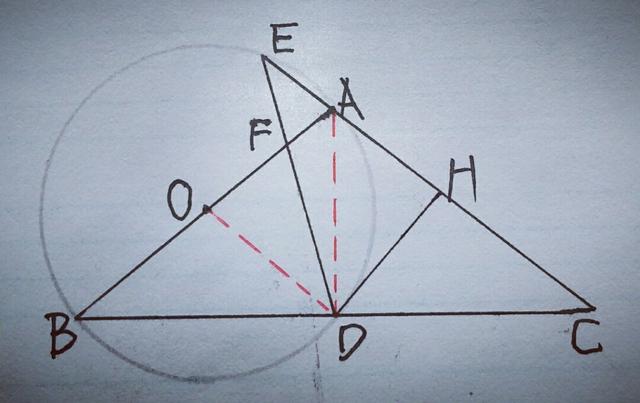
∵AB是⊙O的直径，∴∠ADB=90°，又AB=AC，∴D为BC的中点，则OD为△ABC的中位线，∴OD∥AC，且OD=AC/2，∴∠ODH=∠CHD=90°，∴DH是⊙O的切线.

(2)在⊙O中，∠E=∠B，又∠B=∠C，∴∠E=∠C，又DH⊥EC，∴EH=CH，∵A为EH的中点，可设EA=a，则AH=a，CH=2a，则AC=3a，由(1)知OD∥AC，OD=AC/2=3a/2，∴△FAE∽△FOD，∴EF/FD=EA/OD=a/(3a/2)=2/3.

(3)∵EA=EF=1，∴∠EFA=∠EAF，又∠EFA=∠BFD，∴∠BFD=∠EAF，而∠EAF=∠BDF，∴∠BFD=∠BDF，∴BF=BD，由(1)分析知ED=DC，∴BF=BD=ED=DC，∵OD∥AC，∴∠EAF=∠FOD，∵∠BFD=∠EAF，∴∠FOD=∠BFD，∴OD=FD，设⊙O半径为r，则OD=FD=r，BD=BF=DC=DE=FD+EF=r+1，而BF=OB+OF=r+OF，∴OF=1，我们注意到△FOD∽△FDB，∴FD²=OF×BF，即r²=1×(1+r)，解得r=(1+√5)/2，(负值舍去)，∴⊙O的半径为(1+√5)/2.

第二题相比第一题简单一些，但第(3)问求出OF=1，用半径r表示BF是关键的一环.

【总结】通过上边的两例看出，在进行线段求值的计算中，离不开列方程(可以用相似，三角函数，勾股定理，面积法等列出)，但设参，表示相关线段是最为关键的环节，望同学们用心体会。