中考数学选择题中的有理数、无理数基础

概念：

有理数按其意义分可分为整数和分数，其中整数分为正整数、负整数和0，分数分为正分数和负分数。

有理数按正负来分的话可分为正数、负数和0，其中正数分为正整数和正分数，负数分为负整数和负分数。

这里需注意0即不是正数也不是负数，它只是一个特殊的整数。它能够界分正数和负数。

正数即比0大的数，可以在数字前面加“+”表示，而“+”有时可以不书写。比如在数学中单独的3与+3，都是表示正数3。负数则是与正数相反的概念，是小于0的数，在数字前面加“-”号表示，而且不能省略。

数轴：:规定了原点、正方向和单位长度的直线叫数轴。所有的实数（包括有理数和无理数）都可以用数轴上的点来表示。原点、正方向和单位长度是数轴的3要素缺一不可。

相反数：只有符号不同的两个数互为相反数，互为相反数的两个数绝对值相同。例如：-2与+2互为相反数，且-2和2的绝对值相等。

注意：相反数是两个数间的说法，不能单独说某一个数是相反数，比如不能说2是相反数，但可以说2是-2的相反数；2和-2互为相反数。0的相反数还是0。而求一个数的相反数只需要在其前面加“-”即可。

绝对值：绝对值是指一个数在数轴上所对应点到原点的距离，用“| |”来表示。一般情况下到原点距离相等的数有2个，且两个数互为相反数。但0除外，0到原点的距离是0，所以其绝对值也是0，但只是1个数。

注意：绝对值是表示距离的概念，所以它是恒大于等于0的。

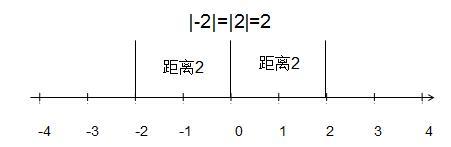
有的学生会疑惑|a|该等于多少，这里教材中有明确的写法。当a≥0时，|a|=a，比如|2|=2，|4/5|=4/5。而当a小于0时，|a|=-a,比如|-2|=-（-2）=2。至于a等于0的情况可以单独分析，也可以合并在大于等于0处，这里便与大于0放在了一起。

倒数： 乘积是1的两个数互为倒数，其中一个数叫做另一个数的倒数。它也是两个数间的概念。但0与任何数相乘都等于0所有0没有倒数，而1与-1的倒数则与其本身相等。0没有倒数；

注意：互为倒数的两个数符号是相同的，即要么都是正数要么都是负数。

运算法则：

加法：⑴同号两数相加，取相同的符号，并把绝对值相加；

⑵绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值；

⑶互为相反数的两数相加，和为零；

加法满足以下定律：

⑴加法交换律：a+b=b+a

⑵加法结合律：(a+b)+c=a+(b+c)

计算时可根据实际情况选择以下顺序做加法：

①互为相反数的两个数先相加——“相反数结合法”；

②符号相同的两个数先相加——“同号结合法”；

③分母相同的数先相加——“同分母结合法”；

④几个数相加得到整数，先相加——“凑整法”；

⑤整数与整数、小数与小数相加——“同形结合法”。

减法与加法相似，减法的计算可看成与符号后的数字相反数间的加法运算。

乘法：

1：两数相乘，同号得正，异号得负，并把绝对值相乘；

2：任何数同0相乘，都得0；

3：几个不是0的数相乘，负因数的个数是偶数时，积是正数；负因数的个数是奇数时，积是负数；

4：几个数相乘，如果其中有因数为0,则积等于0.

乘法运算可应用以下定律：

⑴乘法交换律：ab=ba

⑵乘法结合律：(ab)c=a(bc).

⑶乘法分配律：a(b+c)=ab+ac

除法：

（1）除以一个不等0的数，等于乘以这个数的倒数。

（2）两数相除，同号得正，异号得负，并把绝对值相除。0除以任何一个不等于0的数，都得0。

乘方与开方：

乘方：求n 个相同因数的积的运算，叫做乘方，乘方的结果叫做幂。在a^n中，a 叫做底数，n 叫做指数。

计算规律：

（1）负数的奇次幂是负数，负数的偶次幂的正数。

（2）正数的任何次幂都是正数，0的任何正整数次幂都是0。

开方：开方是指求一个数的方根的运算，它是乘方的逆运算。若一个数b为数a的n次方根，则b^n=a。如果n是偶数，那么负数将没有n次方根。初中阶段一般只涉及2次的平凡根及三次的立方根。

关于开方中，比如3²=（-3）²=9，我们说9的平方根为±3，算术平方根为3。

科学计数法：把一个数表示成 a×10^n的形式或表示成a×10^(-n)的形式（其中，1≤a＜10，n是正整数），这种记数法是科学记数法。

比如： 如：344000可以写成3.44×10^5,0.000031可以表示成3.1×10^(-5)

（数数位，对整数小数点开始默认为在最后一位，往前挪动几位就是乘以10的几次方，反正则是乘以10的负数次方）

下面我们来看一看，中考试题中关于有理数和无理数基础部分，在选择题中是如何考查的（答案写到评论区）：