一、核心知识
1.轴对称图形和两图形成轴对称:
如果把一个图形沿某条直线对折,对折的两部分是完全重合的,那么就称这样的图形为 轴对称图形,这条直线叫做这个图形的对称轴。
把一个图形沿着某一条直线翻折过去,如果它能够与另一图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点叫做对称点。
轴对称图形是对两个图形而言,而成轴对称是 一个图形之间的关系,如果把成轴对称的两个图形看成一个整体,那么它又可看成是一个轴对称图形。
2.轴对称的性质:成轴对称的两个图形 全等;成轴对称的两个图形对应点连线被对称轴 ;
3. 有两条边相等的三角形,叫做等腰三角形;三条边都相等的三角形叫做 等边三角形。
4.等腰三角形的性质:
性质1:等腰三角形的两个两边 相等
性质2:等腰三角形的三线合一
等腰三角形是轴对称图形
5. 等腰三角形的判定:
如果一个三角形有两个相等,那么这两个角所对的边也相等
6.等边三角形的性质:
(1)等边三角形是轴对称图形,且有三条对称轴;
(2)等边三角形的各角相等且每一个角都等于60度;
7.等边三角形的判定:
(1)三条边都相等的三角形是等边三角形.
(2)三个角都相等的三角形是等边三角形.
(3)有一个角等于60°的等腰三角形是等边三角形.
8. 与对称构造有关的直角三角形的性质:
性质一:“在直角三角形中,30°的锐角所对的直角边等于斜边的一半”
性质二:“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°”
二、题型分析
(一)、轴对称性质的简单应用
【例1】如图1,把△ABC纸片沿DE折叠,当点A落在四边形BCED内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请你试着找一找这个规律,你发现的规律是( )
A.∠A =∠1+∠2 B.2∠A =∠1+∠2
C.3∠A =∠1+∠2 D.3∠A =2(∠1+∠2)
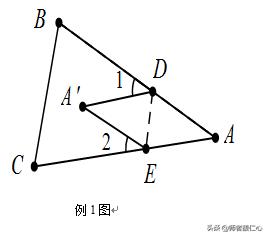
【点拨】考虑把图形还原,则折起的部分与折起前是什么关系呢?
【反思与小结】根据问题的某些特征,运用轴对称思想去添加辅助线,把已知图形的部分或全部补为轴对称形,再利用轴对称性质,常常能较易地从图形各元素的对应关系发现其间的内在联系,找到解题的思路.
(二)、利用轴对称设计图案
【例2】如图是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形.
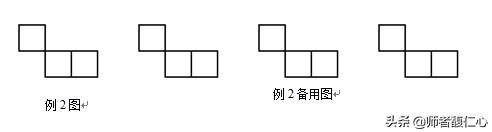
【点拨】小正方形本身就是轴对称图形,而且有四条对称轴,观察图中三个小正方形组成的图形不是轴对称图形,至少需要增画一个小正方形才能组成轴对称图形,思考正方形的对称轴有几条?如何应用对称轴增画一个小正方形使其组成一个轴对称图形?
【反思与小结】每个正三角形有三条对称轴,每个正方形有四条对称轴,每个正边形有条对称轴。本题利用正方形有四条对称轴,分别添画一个正方形使其变成轴对称图形,实际上就是根据正方形四条的对称轴进行添画。
【举一反三】如图甲,正方形被划分成16个全等的三角形,将其中若干个三角形涂黑,且满足下列条件:
(1)涂黑部分的面积是原正方形面积的一半;
(2)涂黑部分成轴对称图形.
如图乙是一种涂法,请在图1~3中分别设计另外三种涂法.(在所设计的图案中,若涂黑部分全等,则认为是同一种涂法,如图乙与图丙.)
【解答】
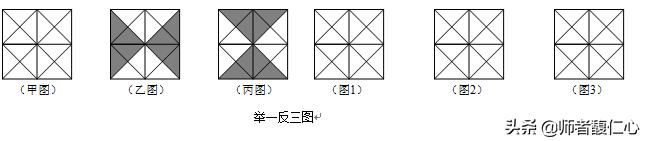
【反思与小结】此类问题主要是利用正方形的轴对称性性质,根据具体要求分类探究。
(三)、轴对称变换与最短路程
【例3】最短路程画图
问题一:如图1,点A、点B在直线的两侧,在直线上画一点P,使得PA+PB最小
问题二:如图2,点A、点B在直线的同侧,在直线上画一点P,使得PA+PB最小
问题三:如图3,在∠AOB内部有一个点定点P,能否分别在OA、OB上画一个点M、N,使得△PMN的周长最小?
若∠AOB=30°,OP=10,求△PMN周长的最小值?
【点拨】(1)思考能否应用线段的性质进行解答?
【解答】

【反思与小结】对于(1)主要是应用线段的性质进行解答;对于(2)是如何应用对称将将七转化为(1)?对于解决(3)中两个动点的问题的策略是令其中的一个动点M(或N)固定,找到合适的点N(或M),再让动点M(或点N)运动,找到合适的答案。也就是说:将(3)转化为问题(1)、(2)的情形。例3是求“最短路程”的重要模型,一定要注意总结归纳提升。
【举一反三(1)】最短路程画图:
从A到B地需要穿过一条河,而河的宽度为,由于经济方面的思考,建造过河的桥要垂直于河的两岸(河的两岸平行),请设计行走路线,使所走的线路的长度最短?
【点拨】对于图1,利用两点之间线段最短容易解决;对于图2,实际行走是“地面上陆地——桥——地面上的陆地”,对于地面上的路可行走直线段,而对于桥,需要走河的宽度,由于是在纸上设计行走路线,能否先走河的宽度,再走陆地上的直线段?那么如何设计线路?
【解答】
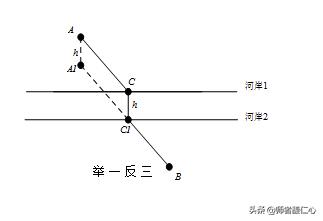
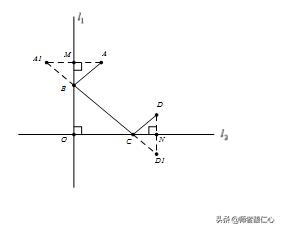
【举一反三(2)】直线⊥,点B在直线上,点C在直线上,A、D是平面上的固定点,请设
计点B、C使得四边形ABCD的周长最小?
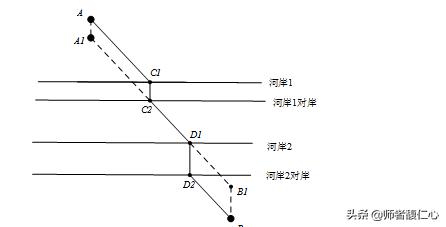
【举一反三(3)】最短路程画图 如图,从A地到B地需要穿过两条河,而河的宽度分别为、,由于经济方面的思考,建造过河的桥要垂直于河的两岸(河的两岸平行),请设计行走路线,使所走的线路的长度最短?
【点拨】能否仿照上题的(2)思考?如何设计?
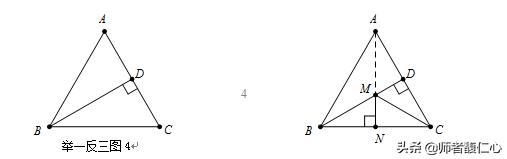
【举一反三(4)】在正△ABC中,BD⊥AC于D,点N在BC上运动,点M在BD上运动,如何设计M、N才能使得CM+MN最短?
(四)、轴对称性质应用与特殊图形面积的求法
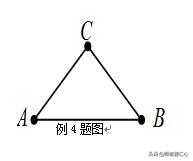
【例4】如图,在△ABC中,∠ACB=90°,AC=BC,AB=a,求△ABC的面积值
【点拨】思考一:要求,需要知道△ABC的底与高,而条件中已知斜边,能否求出斜边上高?
思考二:两个△ABC会组成怎样的图形?能否求出它的面积?四个△ABC会组成怎样的图形?能否求出它的面积【反思与小结】两个全等的等腰直角三角形组成一个大的等腰直角三角形,四个全等的等腰直角三角形能组成一个正方形,而正方形的边就是直角三角形的斜边,容易求出其面积。本题实际上是利用等腰直角三角形和对称的性质进行构造与转
五、简单轴对称图形的构造
【例5】如图,在△ABC中,∠ACB=90°,∠A=30°,求证:BC=AB
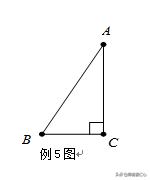
【点拨】思考一:要证:BC=AB,也就是证明AB=2BC,如何构造2 BC,能否应用对称法构造2 BC?
思考二:要证:BC=AB,其中∠A=30°,得到∠B=60°,能否以∠B为其中的一个角构造等边三角形进行证明?
【举一反三】如图,在△ABC中,∠ACB=90°,BC=AB,
求证:∠BAC=30°,
【点拨】思考一:由已知条件BC=AB,能否应用对称法构造2 BC?
思考二:要证明∠A=30°,只要证明∠B=60°问题解决,
能否以∠B为其中的一个角构造等边三角形进行证明?
【反思与小结】要证明倍分问题,一般是采取“加倍法”和“折分法”;本题实际上直角三角形的两个重要性质的证明。
性质一:“在直角三角形中,30°所对的直角边等于斜边的一半”
性质二:“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°”
在证明这两条性质时应用了对折构造的方法。
【例6】如图,在△ABC中,AD⊥BC于D,∠B=2∠C,求证:AB十BD=CD
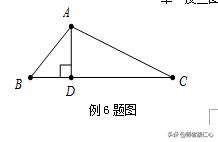
【点拨】要证AB十BD=CD.能否应用“截长补短”?如何“截长”?如何“补短”?
【反思与小结】本题实际上应用了对称变换。通过对称,将某些元素相对集中,从而易于问题的解决。
【例7】在四边形ABCD中,AC平分∠DAB,,过点C作CE⊥AB于E,并且AE=1/2(AB+AD),
求证:∠D+∠ABC=180°
【点拨】由已知AC平分∠DAB,能否利用角平分线构造对称图形,通过对称的性质探究解法?
【反思与小结】角平分线所在直线是角的对称轴。通过角平分线所在直线构造对称图形,利用轴对称图形的性质解答问题,是一种重要辅助线的构造方法。本题利用角平分线,构造全等进而解决问题。
【举一反三】在△ABC中,AD平分∠BAC,M为BC的中点,DM⊥BC于M,
若AB=10,AC=6,DE⊥AB于E,DF⊥AC于F,
①求证:△ADE≌△ADF,②求证:△BDM≌△CDM,③求AE的长度;
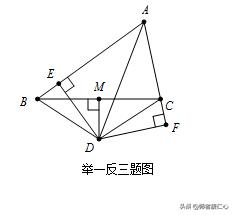
【点拨】对于①、②,由角平分线和垂直平分线的对称性容易得到;
对于③要求AE的长,已知AB、AC的长度,
由全等三角形的性质能否得出AB、AC、AE、AF之间关系?有何关系?
【反思与小结】角平分线所在直线是一个角图形的对称轴。利用角平分线可以构造全等三角形,可以得到线段、角之间的关系。本例是利用角平分线构造全等三角形,从而得到角、线段之间的关系。
【例8】如图,在△ABC中,AC=BC,∠ACB=90°,D是AC上的点,AE⊥DE交BD的延长线于点E,且AE=
求证:BD平分∠ABC
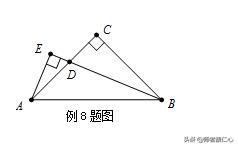
【点拨】要证明:BD平分∠ABC,发现图形给人以“不完整”的感觉,能否将图形成“完整图形”通过构造全等给以证明?
【反思与小结】本题在证明BD平分∠ABC时所构造的辅助线,实际上是在分析的基础上,利用轴对称构造全等三角形进行解答。
三、总结与积累
在轴对称变换下,图形上两点间的距离、角度、面积等保持不变,而这种变换在现实生活中有着广泛的应用和丰富的文化价值.同时通过这种变换,可以使相关的元素相对集中,从而构造新图形,在解决问题中起着出奇制胜的效果. 等腰三角形是以顶角平分线所在直线为对称轴的轴对称图形,等腰三角形的“两底角相等”、“三线合一”等性质是几何证明和计算的重要依据.善于发现、构造等腰三角形,进而利用等腰三角形的性质为解题服务是解几何题的常用技巧.

 加载中,请稍侯......
加载中,请稍侯......
精彩评论