初中数学，一线三角图（K型图）在几何中具有相当重要的位置，常用来证明三角形全等或者相似，善于构造K型图有利于解决几何问题，我们先来看下K型图解决相似三角形的题目。

基本模型图（三垂直）

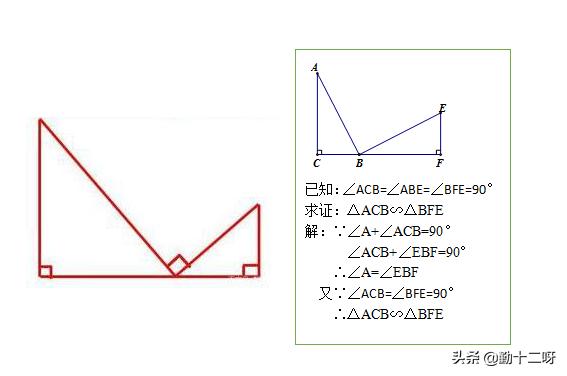
从特殊到一般

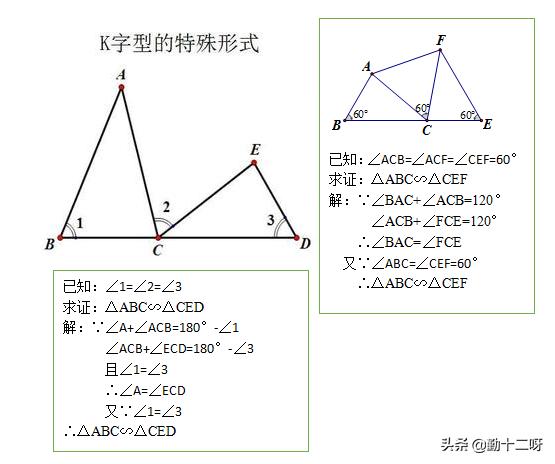
相似中K型图常见形态（A字型、8字型）

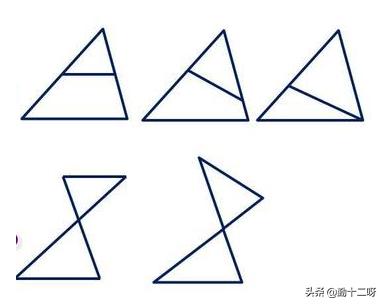
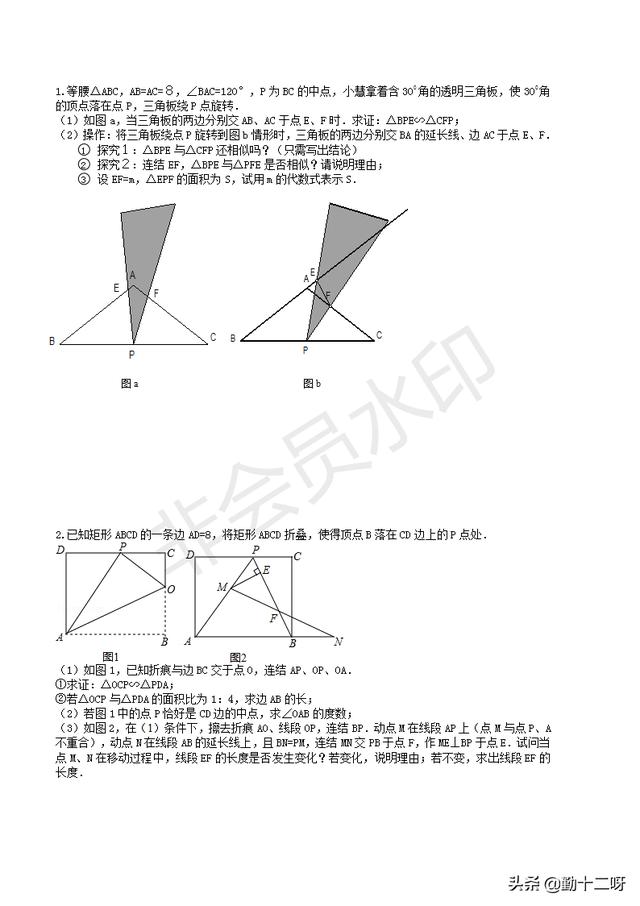
例题1：已知△ABC中AB=AC、BC=8，D是BC边上任意一点，AB边上有一点E，AC边上有一点F，使∠EDF=∠C. 已知BD=6、BE=4，求CF的长。

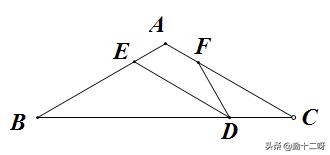
分析：这是一道典型的K型图，已知∠EDF=∠C=∠B，从而可以得到△BDE∽△CFD

例题2：如图，已知点A（0，4）、B（4，1），BC⊥x轴于点C，点P为线段OC上一点，且PA⊥PB．求点P的坐标。

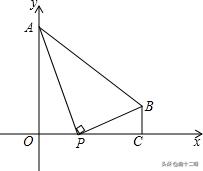
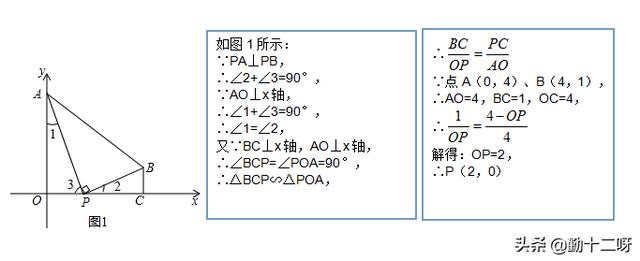
分析：这是三垂直模型图（∠AOP=∠AOB=∠BCP=90°），我们很快可以得到△AOC与△BCP相似

例题3：已知矩形ABCD中，CD=2，AD=3，点P是AD上的一个动点，且和点A，D不重合，过点P作PE⊥CP，交边AB于点E，设PD=x，AE=y，求y关于x的函数关系式，并求出y的最大值。

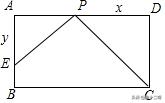
解析：由图可知：∠A=∠EPC=∠D=90°，是三垂直模型，可以得到△EAP∽△PDC，通过比例式得到x与y的函数关系式，进而求出y的最大值

1.由“一线三直角”基本图形搭建桥梁可以得到相似三角形。

2.学习几何最重要是学会归纳一些简单的基本图形，学会从复杂的图形里提炼基本图形，并将其作为解决问题的手段和方法。

3.几何的学习中，要注重图形的运动和变化，总结和发现图形之间的内在联系，探求其规律，帮我们解决繁杂问题