证明线段相等是最常见的几何题,而证明线段的不等关系也会常常遇到,这类题型该怎么考虑?从哪里切入?今天就谈谈这个问题.
首先,若在同一个三角形中,通过定理“三角形任意两边之和大于第三边,任意两边之差小于第三边”可作出判断;当要证的不等关系中的线段,不在同一个三角形中时,可设法构造全等三角形,通过等量代换将它们集中到同一个三角形中,然后利用三角形的三边关系定理加以证明.
下面我们通过三道典型例题来详细探究这个问题:
例1、已知:如下图所示,△ABC中,AB>AC,AD为三角形的中线. 求证:AD<1/2(AB+AC).
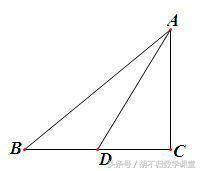
分析:要求证的不等式可以变形为2AD<AB+AC,需将2AD,AB,AC三线段集中到同一个三角形中,为此,如下图所示,延长AD到E,使DE=AD,则AE=2AD,这样问题就转化为证AE<AB+AC即可. 连接CE,则由SAS定理可证得△ABD≌△ECD,所以EC=AB. 于是三条线段就集中到△AEC中,由三角形三边关系定理便可推出结论.
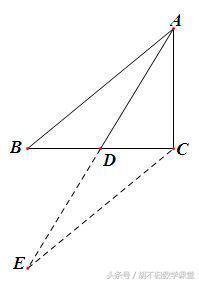
点评:要把证明的线段集中到同一个三角形中是解决问题的关键,是战略思想,然后“见中点,要倍长,倍长之后证全等”是具体步骤,知行合一,从而得到解决问题的钥匙.
例2、如下图所示,△ABC中,AB=AC,D是AB上一点,延长AC到E,使CE=BD,DE交BC于点F. 求证:DE>BC.
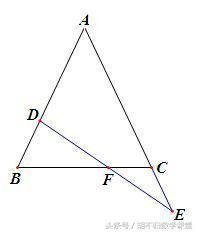
分析:要证DE>BC,即证DF+FE>BC. 因此,需构造一个三角形,使线段DF、EF、BC为这个三角形的三边.
如下图,延长FB到G,使BG=CF,连接DG. 由SAS可证得△BDG≌△CEF,所以DG=EF,在△DFG中,有DF+DG>GB+BF,所以DF+EF>CF+BF,即DE>BC.
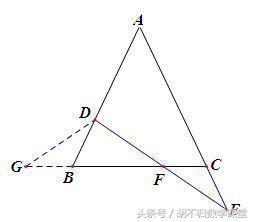
点评:设法把要证的边转化到同一个三角形中是解决问题的关键.
例3、已知:如下图所示,在△ABC中,AB>AC,AD为∠A的平分线,P为AD上任意一点. 求证:PB-PC<AB-AC.
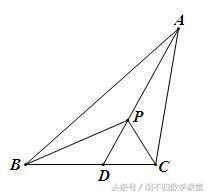
分析:要证的不等式是两边之差,故可联想三角形两边之差小于第三边的定理,若把AB-AC变成一个三角形的边将是很好的一个思路. 在AB上截取AE=AC,则BE=AB-AC. 这样PB、BE在同一个三角形中,即PB与AB-AC在△BPE中,若能证出PE=PC,问题就可以解决. 因为AD为∠A的平分线,AE=AC,很容易由SAS定理证得△APE≌△APC,所以PE=PC,问题得到解决.
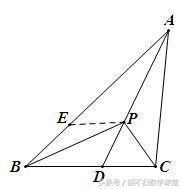
点评:当所证的式子中多于三条线段,常需截长补短,作出线段差或线段和,构造全等三角形,将它们集中在同一三角形中,利用三角形两边之和大于第三边,或两边只差小于第三边来证明.
【配套练习】
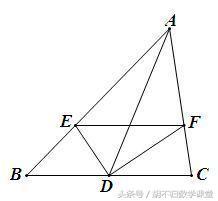
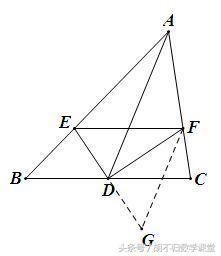
1、已知:如下图,AD是△ABC的中线,∠ADB、∠ADC的平分线分别交AB、AC于点E、F. 求证:BE+CF>EF.
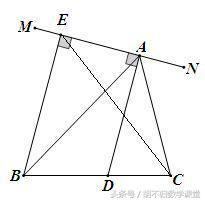
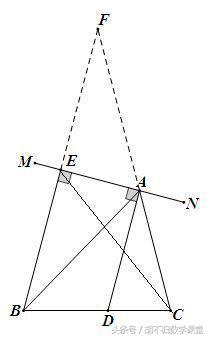
2、已知:如下图,AD为△ABC的角平分线,过A引直线MN⊥AD,过B作BE⊥MN于点E. 求证:EB+EC>AB+AC.
【答案】
1、如下图,延长ED到G,使DG=ED,连接FG,证FG=EF,GC=BE,∵ CG+CF>EG,∴ BE+CF>EF.
2、如下图,在CA延长线上截取AF=AB,连接FE,证FE=BE ∵ FE+EC>FC,∴ EB+EC>AB+AC.

 加载中,请稍侯......
加载中,请稍侯......
精彩评论