中考压轴题之 ——平面直角坐标系下的角度相等问题

中考题最后的压轴题中，经常出现与角度相关的问题。与平面直角坐标系结合，将三角形全等、三角形相似、三角函数、圆及二次函数等知识有机的结合在一起，考察学生对知识综合、灵活应用的能力，同时考察学生解题方法的思路的灵活性，以及对数学学科思维的掌握情况。

平面直角坐标系下的角度相等问题，通常有以下几种解题思路：

1、 利用三角形全等解决

2、 利用三角形相似解决

3、 利用三角函数解决

4、 利用圆的知识解决

下面分类举例说明：

类型一、 利用三角形全等解决角度相等问题

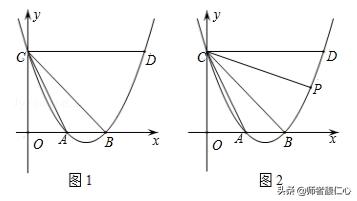
例1、如图，抛物线y＝ax2+bx+3（a≠0）与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C，连接BC．

（1）求抛物线的表达式；

（2）点D（2，m）在第一象限的抛物线上，连接BD．在对称轴左侧的抛物线上是否存在一点P，满足∠PBC＝∠DBC？如果存在，请求出点P的坐标；如果不存在，请说明理由．

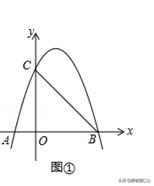
【解析】：（1）∵抛物线y=ax^2+bx+3（a≠0）与x轴交于点A（-1，0），B（3，0），带入两点坐标即可。

∴抛物线的表达式为y=-x^2+2x+3；

(2) 设BP交轴y于点G，再根据点B、C、D的坐标，得到∠DCB=∠OBC=∠OCB=45°，进而判定△CGB≌△CDB，求得点G的坐标为（0，1），得到直线BP的解析式为y=- 1/3x+1，最后计算直线BP与抛物线的交点P的坐标即可．

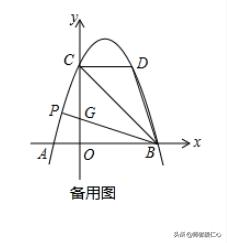
【解答】解：（1）抛物线的表达式为y=-x^2+2x+3；(过程略）

（2）存在．

如图，设BP交轴y于点G，

∵点D（2，m）在第一象限的抛物线上，

∴当x＝2时，m＝﹣2^2+2×2+3＝3，

∴点D的坐标为（2，3），

把x＝0代入y＝﹣x^2+2x+3，得y＝3，

∴点C的坐标为（0，3），

∴CD∥x轴，CD＝2，

∵点B（3，0），

∴OB＝OC＝3，

∴∠OBC＝∠OCB＝45°，

∴∠DCB＝∠OBC＝∠OCB＝45°，

又∵∠PBC＝∠DBC，BC＝BC，

∴△CGB≌△CDB（ASA），

∴CG＝CD＝2，

∴OG＝OC﹣CG＝1，

∴点G的坐标为（0，1），

设直线BP的解析式为y＝kx+1，

将B（3，0）代入，得3k+1＝0，

解得k＝﹣1/3，

∴直线BP的解析式为y＝﹣1/3x+1，

令﹣1/3x+1＝﹣x^2+2x+3，

解得x1=-2/3，x2＝3，

∵点P是抛物线对称轴x＝1左侧的一点，即x＜1，

∴x＝﹣2/3，

把x＝﹣2/3代入抛物线y＝﹣x^2+2x+3中，

解得y＝11/9，

∴当点P的坐标为（﹣2/3，11/9）时，满足∠PBC＝∠DBC．

【总结】出现角等的条件时，可以将两角构造在全等三角形中，利用全等的性质解决问题。

类型二：利用三角形相似解决角度相等问题

例2 、如图，在平面直角坐标系xOy中，抛物线y=x^2+bx+c与y轴交于点C，与x轴交于A，B两点，点B的坐标为（3，0），直线y=﹣x+3恰好经过B，C两点

（1）写出点C的坐标；

（2）求出抛物线y=x2+bx+c的解析式，并写出抛物线的对称轴和点A的坐标；

（3）点P在抛物线对称轴上，抛物线顶点为D且∠APD=∠ACB，求P坐标．

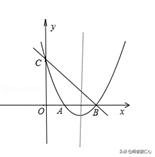
【分析】（1）由直线y＝﹣x+3可求出C点坐标；

（2）由B，C两点坐标便可求出抛物线方程，从而求出抛物线的对称轴和A点坐标；

（3）因为P在对称轴上，D为抛物线顶点，所以 PD垂直于x轴。△AFP为直角三角形。若∠APD=∠ACB，则作出辅助线AE垂直于BE，由三角形的两个角相等，证明△AEC∽△AFP。线段AE、CE、AF都可求，根据两边成比例，便可求出PF的长度，从而求出P点坐标．

【解答】解：（1）y＝﹣x+3与y轴交于点C，故C（0，3）．

（2）∵抛物线y＝x2+bx+c过点B，C，析式为y＝x^2﹣4x+3

∴对称轴为x＝2，点A（1，0）．

（3）由y＝x^2﹣4x+3，

可得D（2，﹣1），A（1，0），

∴OB＝3，OC＝3，OA＝1，AB＝2，

可得△OBC是等腰直角三角形，

∴∠OBC＝45°，BC=3根2

如图，设抛物线对称轴与x轴交于点F，

∴AF＝1/2AB＝1．

过点A作AE⊥BC于点E．

∴∠AEB＝90度．

可得，BE=AE= 根2， CE=2根2

在△AEC与△AFP中，∠AEC＝∠AFP＝90°，∠ACE＝∠APF，

∴△AEC∽△AFP．

∴AE/AF=CE/PF

解得PF＝2．

或者直接证明△ABC∽△ADP得出PD＝3，

再得PF＝2．

∵点P在抛物线的对称轴上，

∴点P的坐标为（2，2）或（2，﹣2）．

【总结】出现角等的条件时，可以将两角构造在相似三角形中，利用相似对应边成比例的性质解决问题。这类问题也可以用三角函数解决。见类型三。

类型三、利用三角函数解决角度相等问题

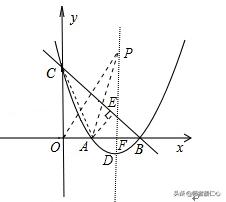
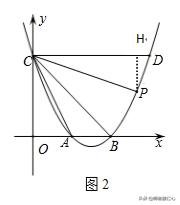
例3、（2018•济南中考题改编）如图1，抛物线y＝ax^2+bx+4过A（2，0）、B（4，0）两点，交y轴于点C，过点C作x轴的平行线与抛物线上的另一个交点为D，连接AC、BC．点P是该抛物线上一动点，设点P的横坐标为m（m＞4）．

（1）求该抛物线的表达式和∠ACB的正切值；

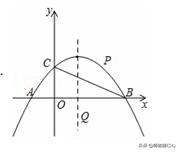
（2）如图2，若∠ACP＝45°，求m的值；

【解析】（1）由点A、B坐标利用待定系数法求解可得抛物线解析式为y＝1/2x^2﹣3x+4，作BG⊥CA，交CA的延长线于点G，证△GAB∽△OAC，据此知BG＝2AG．在Rt△ABG中根据BG^2+AG^2＝AB^2，可求得AG．继而可得BG，CG，根据正切函数定义可得答案；

（2）由题意可得，∠BCD=45°，若∠ACP＝45°，则∠ACB=∠PCD。即tan∠ACB=tan∠PCD。由（1）得tan∠ACB=1/3，所以tan∠PCD=1/3。过P做PH⊥CD于点H，设出P点坐标，列方程即可。

【解答】(1) 略tan∠ACB=1/3

（2）∵∠BCD=45°

若∠ACP＝45°，

则∠ACP=∠PCD。

即tan∠ACP=tan∠PCD。

由（1）得tan∠ACB=1/3，

∴tan∠PCD=1/3。

过P做PH⊥CD于点H

设P（m，1/2m^2﹣3m+4）

则HC=m PH=4-1/2m^2+3m-4=-1/2m^2+3m

∵tan∠PCD=1/3

∴ PH/HC=1/3

即（-1/2m^2+3m）/m=1/3

解得：m=16/3 或m=0（舍去）

∴ m=16/3

【总结】出现角等的条件时，即两个角的正切值相等。从而列出方程解决即可。这类问题也可以用相似解决，见类型二。

类型四：利用隐圆解决角度相等问题

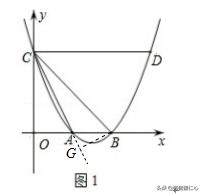
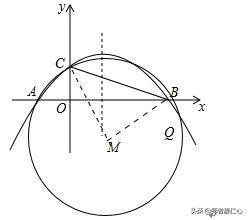
例4、（2018 日照中考题改编）如图，点A（﹣1，0），B（3，0），C（0，1）在抛物线y=ax^ 2+bx+c上．

（1）求抛物线解析式；

（2）在x轴下方且在抛物线对称轴上，是否存在一点Q，使∠BQC=∠BAC？若存在，求出Q点坐标；若不存在，说明理由．

【解析】（1）设抛物线的解析式为y＝a（x+1）（x﹣3），将C（0，1）代入求得a的值即可

（2）首先依据点A和点C的坐标可得到∠BQC＝∠BAC＝45°，设△ABC外接圆圆心为M，则∠CMB＝90°，设⊙M的半径为x，则Rt△CMB中，依据勾股定理可求得⊙M的半径，然后依据外心的性质可得到点M为直线y＝﹣x与x＝1的交点，从而可求得点M的坐标，然后由点M的坐标以及⊙M的半径可得到点Q的坐标．

【解答】解：（1）设抛物线的解析式为y＝a（x+1）（x﹣3），将C（0，1）代入得﹣3a＝1，解得：a＝﹣1/3，

∴抛物线的解析式为y＝﹣1/3x^2+x+1．

（3）存在．

∵A（﹣1，0），C（0，1），

∴OC＝OA＝1

∴∠BAC＝45°．

∵∠BQC＝∠BAC＝45°，

∴点Q为△ABC外接圆与抛物线对称轴在x轴下方的交点．

设△ABC外接圆圆心为M，则∠CMB＝90°．

设⊙M的半径为x，则Rt△CMB中，由勾股定理可知CM^2+BM^2＝BC^2，即2x^2＝10，解得：x＝根5（负值已舍去），

∵AC的垂直平分线的为直线y＝﹣x，AB的垂直平分线为直线x＝1，

∴点M为直线y＝﹣x与x＝1的交点，即M（1，﹣1），

∴Q的坐标为（1，﹣1﹣根5）．

【总结】出现角等的条件时，根据题目出现的条件，利用同弧所对的圆周角相等或同弧的圆周角是圆心角的一半，构造圆形解决问题。