函数零点问题的4种解题方法
一、依据概念 化为方程求根
对于函数y=f(x),我们把f(x)=0使的实数x叫做函数y=f(x)的零点,因此,该方法就是将函数的零点问题转化为方程f(x)=0的问题来解答。
二、由数到形实现零点交点的互化
函数y=f(x)的零点,即函数y=f(x)的图像与x轴的交点的横坐标。因此,求函数的零点问题可转化为函数y=f(x)图像与x轴的交点的横坐标,或将方程f(x)=0整理成f1(x)=f2(x)形式,然后在同一直角坐标系下,画出两函数的图像,交点的横坐标即为函数的零点,交点的个数即为函数的零点个数。
注:在解题中,若遇到函数形式复杂难以作图时,则不妨先整理表达式,一般以所涉及的函数能作其图像为整理要求。接着在同一坐标系下,规范作图,然后确定交点的位置或个数,特别在部分区间上是否存在交点,要细心对待,有时还需计算相关的函数值(函数值的趋势)来确定是否有交点。
三、依存定理 凭号而论
如果函数y=f(x)在区间[a,b]上的图像时联系不断的一条曲线,并且有f(a)f(b)<0,那么函数y=f(x)在区间(a,b)内有零点。即存在c∈(a,b),使得f(c)=0。通常将此论述称为零点存在性定理。因此,该解题策略就是将函数零点分布问题转化为判断不等式f(a)f(b)<0是否成立。
四、借助单调 确定问题
如果函数y=f(x)在区间[a,b]上的图像时连续不断的一条具有单调性曲线,并且有f(a)f(b)<0,那么函数y=f(x)在区间(a,b)内有唯一零点,即存在唯一的c∈(a,b),使得f(c)=0。通常将此论述称为零点唯一性定理。因此,该策略解题需要考虑两个条件:条件一是f(a)f(b)<0是否成立;条件二是否具有单调性。
题型一:已知零点个数求参数范围


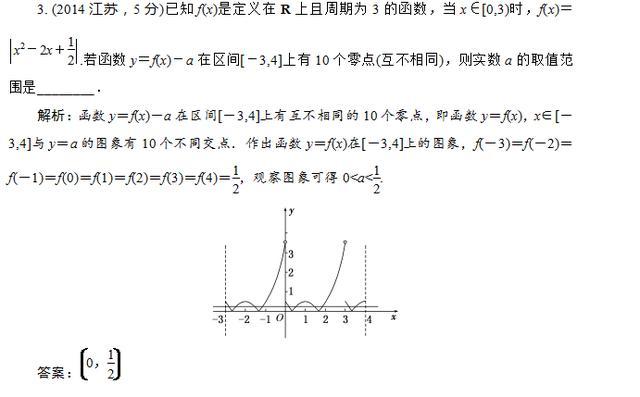

题型二:求零点所在区间




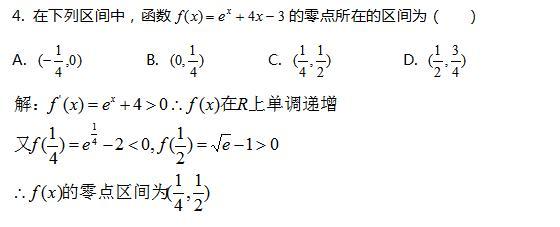

题型三:求零点个数






 加载中,请稍侯......
加载中,请稍侯......
精彩评论