平抛运动可以看成是水平方向做匀速运动,竖直方向做自由落体运动的这两种运动的合运动。
解决问题的方法是:根据题意,正确地作出示意图,识别出运动性质后,将平抛运动分解成直线运动,运用相关的运动规律(公式),列出方程解出结果。
一、运用平抛运动规律解题
例1、如图1所示,两个相对的斜面,倾角分别为37°和53°。在顶点把两个小球以同样大小的初速度分别向左、右水平抛出,小球都落在斜面上。若不计空气阻力,则A、B两个小球的运动时间之比为( )。
A. 1:1
B. 4:3
C. 16:9
D. 9:16
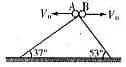
图1
解析:设作平抛运动物体运动的时间为t,则位移的水平分量和竖直分量分别为
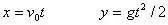
而由图可知
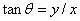
故
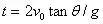
所以有
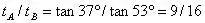
即D选项正确。
二、平抛运动问题正误辨析
例2、如图2所示,AB为斜面,BC为水平面。从A点以水平速度v向右抛出一小球,其落点与A的水平距离为S1;从A点以水平速度2v向右抛出另一小球,其落点与A的水平距离为S2。不计空气阻力,则S1:S2可能为( )。
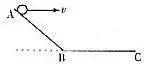
图2
A. 1:2
B. 1:3
C. 1:4
D. 1:5
分析:根据平抛运动的基本公式
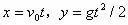
可推得水平位移与初速度成正比,所以误认为选项A正确。此题对选项B的判断用到临界法,确定了两种情况平抛运动的解,介于两者之间的也是符合题意的解。不要忽略了落点在斜面上的情况。
解:要考虑到落至斜面和落至平面上的不同情况。若两次都落在平面上,则A对;若两次都落在斜面上,则C对;若第一次落在斜面上,第二次落在平面上,B就可能正确,其实只要介于1:2和1:4之间都可以,所以正确选项应为A、B、C。
例3、如图3所示,一高度为
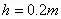
的水平面在A点处与一倾角为θ=30°的面连接。一小球以
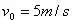
的速度在平面向右运动。求小球从A点运动到地面所需要的时间(平面与斜面均光滑,取
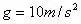
)。

图3
某同学对此题的解法为:小球沿斜面运动,则
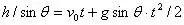
由此可求得落地的时间t。
问:你同意上述解法吗?若同意,求出所需要的时间;若不同意,则说明理由并求出你认为正确的结果。
解析:不同意。小球应在A点离开平面做平抛运动,而不是沿斜面下滑。落地与A点的水平距离
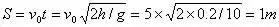
斜面底宽
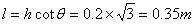
因为
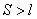
,所以小球离开A点不会落到斜面,因此落地时间为平抛运动时间,故
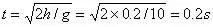
三、平抛运动实验图表处理
例4、在研究平抛物体运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长L=1.25m。若小球在平抛运动途中的几个位置如图4所示的a、b、c、d,则小球平抛的初速度的计算公式为
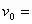
__________(用L、g表示),其值是_________(取
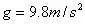
)。
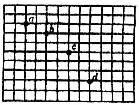
图4
分析:这是一道难度较大的题,据以往的错解情况,不少同学都是误将a点作为抛出点,很快地利用
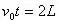
及
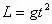
求解得错误答案
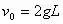
。另外此题在竖直方向上也可用处理纸带的方法:利用
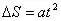
来求解更为简单。
解析:由图可以看出:a、b、c、d各位移水平间隔相等,即小球下落到各位置间时间间隔相等,设为t;则初速度为
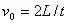
。
考虑物体由a到b及由b到c过程的竖直分运动,有
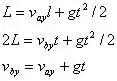
联立以上四式解得
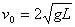
代入数据得
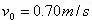
四、类平抛运动
例4、质量为m的飞机以水平速度v0飞离跑道后逐渐上升。若飞机在此过程中水平速度保持不变,同时受到重力和竖直向上的恒定升力(该升力由其他力的合力提供,不含重力)。今测得当飞机在水平方向的位移为
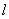
时,它的上升高度为h,如图5所示。求飞机受到的升力的大小。
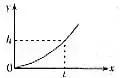
图5
分析:合外力F恒定,且与物体初速度
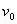
方向垂直,此运动称之为类平抛运动,其运动轨迹为抛物线,处理方法和平抛运动类似(运动分解)。该题属于方法迁移题,学生需要理解平抛运动的处理方法,才能进一步灵活地处理该问题。
解析:因飞机上升到h高度的时间为t;有
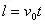
y方向加速度为
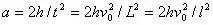
设飞机的升力为F,由牛顿第二定律有
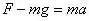
故
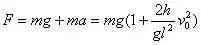

 加载中,请稍侯......
加载中,请稍侯......
精彩评论