经典再现11——弦之和最大值问题的常见解法

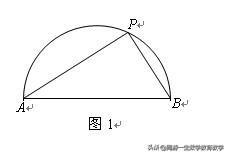
题：如图1，已知半圆O的直径AB=2，P是弧AB上的动点，求PA+PB的最大值．

分析：一见到动点到两个定点距离之和最值问题，大多数人马上就会想到“将军饮马”问题，但“将军饮马”问题中动点是在直线上，求的是线段和的最小值，而这里的动点是在圆弧上，欲求的是最大值，显然与“将军饮马”问题恰好相反，由此可见两者是没有可比性的．怎么办呢？调动一切与最大值有关的性质、定理、公式和方法．

首先，注意到AB是半圆的直径，所以∠APB=90°，因此，这个问题就相当于已知直角三角形的斜边，求三角形周长的最大值，这为勾股定理和三角函数的运用提供了广阔的思维空间．

思路一：根据勾股定理，PA、PB的长是互相制约的，如果PA的长确定了，PB的长也随之确定．因此，以PA为变量，建立PA+PB与PA的等量关系——一元二次方程，再根据根的判别式进行求解．

解法1：设PA=x，PA+PB=y，则PB=√(4-x^²)，

所以y=x+√(4-x^²)，y-x=√(4-x^²)，

两边平方，并整理，得

2x^²-2yx+y^²-4=0，

因为x、y是实数，

所以△=(-2y)^²-4×2×(y^²-4)≥0，

整理，得y^²≤8，

因为y为正数，所以y≤2√2，

所以y最大值为2√2，

即PA+PB最大值为2√2.

思路二：运用数形结合思想，利用图形直观性求PA+PB平方的最大值．

解法2：设PA+PB=y，则

y^²=(PA+PB)^²

=PA²+PB^²+2PA·PB，

因为∠APB=90°，

所以PA²+PB^²= AB²=4，

PA·PB=2S_△ABC，

所以y^²=4+4 S_△ABC.

作高PC（如图2），则

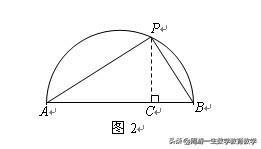
S_△ABC=1/2·AB·PC=PC，

显然，当点P为弧AB中点时，

PC最大=圆的半径1，

所以S_△ABC的最大值为1，

所以y^²的最大值为4+4=8，

因为y为正数，

所以y最大值为√8=2√2，

即PA+PB最大值为2√2.

思路三：因为PA、PB的大小决定于点P的位置，而点P的位置决定于∠A的大小，因此，运用三角函数，将PA+PB转化为∠A的三角函数后再求解．

解法3：由三角函数，得

PA=AB·cosA=2cosA，

PB=AB·sinA=2sinA，

所以PA+PB=2(cosA+sinA)

=2√(cosA+sinA)^²

=2√(sin^²A+cos^²A+2sinAcosA)

=2√(1+2sinAcosA)

=2√[2-(1-2sinAcosA)]

=2√[2-( sin^²A+cos^²A -2sinAcosA)]

=2 √[2-( sinA-cosA)^²)]

≤2√(2-0)=2√2.

所以PA+PB最大值为2√2.

思路四：将PA、PB合并为一条，再依据具体情况确定解决方法．

解法4：如图3，延长AP到C，使PC=PB，连接BC．则

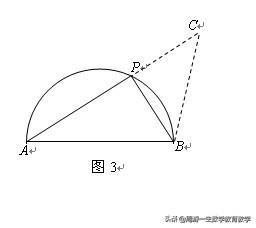
PA+PB=AC，△PBC是等腰直角三角形，∠C=45°，

在△ABC中，由正弦定理，得

AC/sin∠ABC=AB/sinC=2/sin45°=2√2，

所以AC=2√2sin∠ABC，

因为sin∠ABC≤1,

所以AC≤2√2，AC最大值为2√2

所以PA+PB的最大值为2√2．

思路五：在解法4的基础上，将CB延长交另一半圆于点D，既可以把PA、PB合二为一，又可以将合并后的线段转化为弦．

解法5：延长AP到C，使PC=PB，连接CB，并延长交圆于另一点D，连接AD（如图4）．则

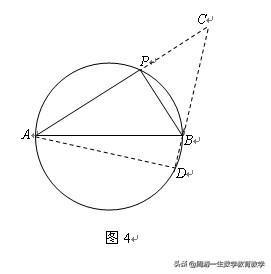
PA+PB=AC，△PBC是等腰直角三角形，∠C=45°，

因为AB为直径，所以∠D=90°，

所以△ACD是等腰直角三角形，

所以AC=√2AD，

因为AD是弦，所以AD≤AB=2，

所以AC≤2√2，即AC最大值为2√2，

所以PA+PB最大值为2√2.

思路六：仿照解法3，直接将PA+PB转化为PA-PB进行求解．

解法6：PA+PB=√(PA+PB)^²

=√(PA^²+PB^²+2PA·PB)

=√[2(PA^²+PB^²)-( PA^²+PB^²-2PA·PB)]

=√[2·4-(PA-PB)^²]

≤√(8-0)（当PA=PB时，等号成立）

=2√2，

即PA+PB≤2√2，

所以PA+PB最大值为2√2.

从以上各种解法可以对解决最大值问题的有关数学知识与方法有如下几种：

（1）正弦最大值为1；

（2）最长的弦是直径；

（3）弧的中点到弦的距离最大；

（4）配方法；

（5）判别式法．