几何证明和计算题是七年级数学的一个重点，因为刚接触这门学科，很多学生反映不知道如何着手分析解题，为了帮助学生们快速掌握学会这类题型，本文就几个典型例题详细讲解解题思路和解题全过程。

例题1

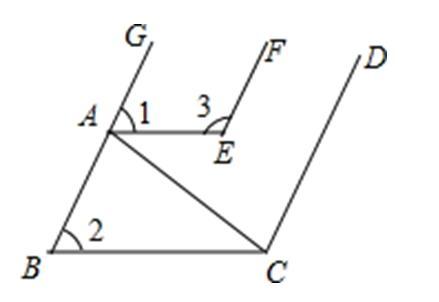
如图，已知：点A在射线BG上，∠1=∠2，∠1+∠3=180°，∠EAB=∠BCD．

求证：EF∥CD．

1、根据需要证明的结论添加辅助线

证明：EF∥CD,需要构造同位角、内错角或同旁内角，因此考虑添加辅助线，延长AE交CD于M。

2、根据需要证明的结论反推需要先证明的结论

证明：EF∥CD，需要先证明∠3=∠EMD;

根据题目中的条件：∠1+∠3=180°，需要先证明∠EMD +∠3=180°;

根据平行线的性质：两直线平行，同旁内角互补，需要先证明BG∥CD。

3、根据题目中的条件推断可以得到的结论

由题目中的条件：∠1=∠2，根据平行线的判定：同位角相等，两直线平行，则AE∥BC；

根据平行线的性质：两直线平行，同旁内角互补，则∠EAB+∠2=180°；

根据题目中的条件：∠EAB=∠BCD，则∠BCD+∠2=180°;

根据平行线的判定：同旁内角互补，两直线平行，则BG∥CD。

4、具体证明过程

延长AE交CD于M

∵∠1=∠2

∴AE∥BC

∴∠EAB+∠2=180°

∵∠EAB=∠BCD

∴∠BCD+∠2=180°

∴BG∥CD

∴∠1+∠EMD=180°

∵∠1+∠3=180°

∴∠EMD=∠3

∴EF∥CD

例题2

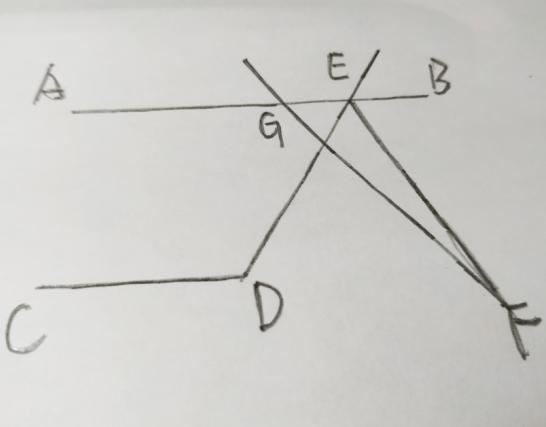
如图，AB∥CD，∠CDE=119°，GF交∠DEB的平分线EF于点F，∠AGF=130°，求∠F

1、根据题目需要求解的值反推需要先求解的值

需要求解∠F，由题目中的条件：∠AGF为△EFG的外角，根据三角形外角的性质：三角形的外角等于不相邻两个内角的和，则∠AGF=∠AEF+∠F，即∠F=∠AGF-∠AEF，

因此，需要先求解∠AEF；

根据题目中的条件：∠AEF=∠AED+∠DEF，需要先求解∠AED，∠DEF；

由题目中的条件EF为∠DEB的平分线，根据角平分线的性质：角平分线可以得到两个相等的角，则∠DEF=1/2∠DEB，因此需要先求解∠DEB。

2、根据题目中的条件推论可以求解的值

由题目中的条件：AB∥CD，∠CDE=119°，根据平行线的性质：两直线平行，同旁内角互补，则∠AED+∠CDE=180°，即∠AED = 180°-∠CDE=61°；

由题目中的条件：AB∥CD，∠CDE=119°，根据平行线的性质：两直线平行，内错角相等，则∠DEB=∠CDE，即∠DEB =119°。

3、具体解题过程

∵AB∥CD，∠CDE=119°

∴∠DEB=∠CDE=119°

∵EF为∠DEB的平分线

∴∠DEF=1/2∠DEB=59.5°

∵AB∥CD，∠CDE=119°

∴∠AED+∠CDE=180°

∴∠AED = 180°-∠CDE=61°

∴∠AEF=∠AED+∠DEF=120.5°

在△EFG中

∵∠AGF为△EFG的外角

∴∠AGF=∠AEF+∠F

∴∠F=∠AGF-∠AEF

∵∠AGF=130°

∴∠F=9.5°

例题3

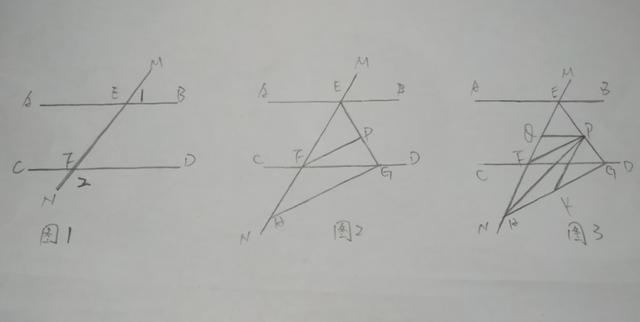
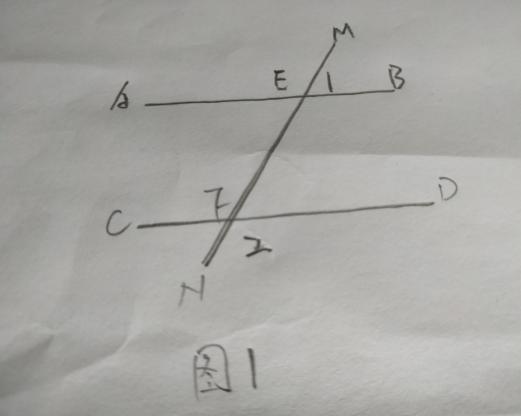
如图1，直线MN与直线AB、CD分别交于点E、F，∠1与∠2互补；

（1）试判断直线AB与直线CD的位置关系，并说明理由；

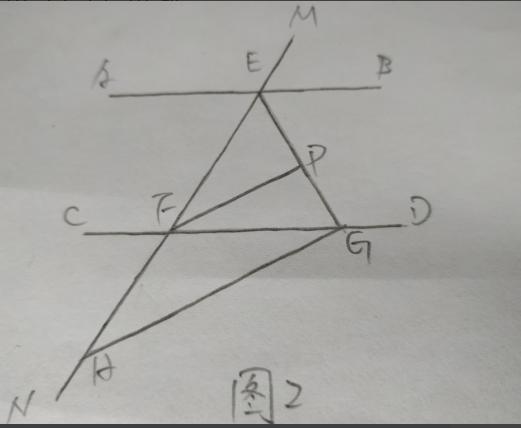
（2）如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH；

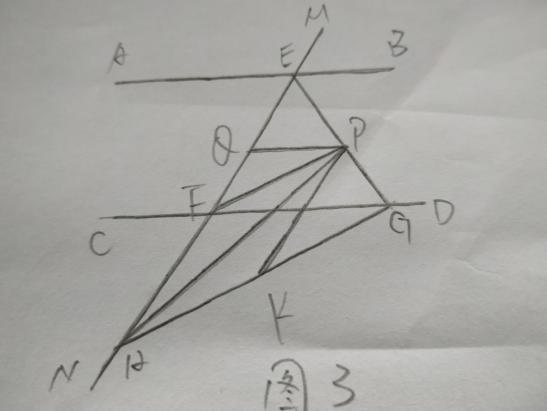
（3）如图3，在（2）的条件下，连接PH，K是GH上一点使∠PHK=∠HPK，作PQ平分∠EPK，求∠HPQ。

一、证明（1）的结论：AB∥CD

1、根据需要证明的结论反推需要先证明的结论

证明：AB∥CD，需要先找同位角、内错角、或同旁内角;

根据平行线的判定：同位角相等，两直线平行，需要先证明∠1=∠MFD。

2、根据题目中的条件推断可以得到的结论

根据题目中的条件：∠1与∠2互补，∠MFD与∠2互补，则∠1+∠2=180°，∠MFD+∠2=180°；

根据补角的性质：同角的补角相等，则∠1=∠MFD。

3、具体证明过程

∵∠1与∠2互补，∠MFD与∠2互补

∴∠1=∠MFD

∴AB∥CD

二、证明（2）的结论：PF∥GH

1、根据需要证明的结论反推需要先证明的结论

证明：PF∥GH，需要找同位角、内错角、或同旁内角;

根据平行线的判定：同位角相等，两直线平行，需要证明∠FPE=∠HGE；

由题目中的条件：GH⊥EG，则∠HGE=90°，需要证明∠FPE=90°;

根据三角形内角和定理：在△EFP中，∠FPE+∠EFP+∠FEP=180°，需要证明∠EFP+∠FEP=90°

2、根据题目中的条件推断可以得到的结论

由（1）的结论：AB∥CD，根据平行线的性质：两直线平行，同旁内角互补，则∠BEF+∠EFD=180°;

由题目中的条件：EP、FP分别为∠BEF与∠EFD的角平分线，根据角平分线性质：角平分线可以得到两个相等的角，则∠EFP+∠FEP =1/2∠EFD+1/2∠FEB=90°。

3、具体证明过程

∵AB∥CD

∴∠BEF+∠EFD=180°

∵EP、FP分别为∠BEF与∠EFD的角平分线

∴∠EFP =1/2∠EFD，∠FEP=1/2∠FEB

∴∠EFP+∠FEP =1/2∠EFD+1/2∠FEB=90°

∵∠FPE+∠EFP+∠FEP=180°

∴∠FPE=180°-（∠EFP+∠FEP）=90°

∵GH⊥EG

∴∠HGE=90°

∴∠FPE=∠HGE

∴PF∥GH

三、求∠HPQ

1、根据题目需要求解的值反推需要先求解的值

需要求解∠HPQ，根据题目中的条件：∠HPQ =∠QPK-∠HPK，需要先求解∠QPK、∠HPK；

由题目中的条件：PQ平分∠EPK，根据角平分线的性质：角平分线可以得到两个相等的角，则∠QPK =1/2∠EPK，需要先求解∠EPK；

由题目中的条件：∠EPK=∠EPF+∠FPK，∠EPF=90°，需要先求解∠FPK；

因此需要证明∠HPK与∠FPK的关系。

2、根据题目中的条件推论可以求解的值

由（2）的结论：PF∥GH，根据平行线的性质：两直线平行，内错角相等，则∠FPH=∠PHK；

根据题目中的条件：∠PHK=∠HPK，则∠FPH=∠HPK，即∠FPH=∠HPK=1/2∠FPK；

由题目中的条件：PQ平分∠EPK，根据角平分线的性质：角平分线可以得到两个相等的角，则∠QPK =1/2∠EPK=1/2（∠EPF+∠FPK）；

由题目中的条件：∠EPF=90°，则∠QPK=1/2（90°+∠FPK）=45°+∠FPH；

由题目中的条件：∠HPQ =∠QPK-∠HPK，则∠HPQ=45°+∠FPH-∠FPH=45°。

3、具体求解过程

∵PF∥GH

∴∠FPH=∠PHK

∵∠PHK=∠HPK

∴∠FPH=∠HPK=1/2∠FPK

∵PQ平分∠EPK

∴∠QPK =1/2∠EPK=1/2（∠EPF+∠FPK）=1/2（90°+∠FPK）=45°+∠FPH

∴∠HPQ =∠QPK-∠HPK=45°+∠FPH-∠FPH=45°

总之，几何的证明和计算题是初中数学的重要题型，只要根据题意认真分析、灵活运用各种性质定理，就能顺利攻克这类题型，轻松掌握重要知识点，实现七年级的几何入门。