在《浮力》这一章里，我们可以建立一套“422模型”，方便我们解决问题。

其中“4”指的的是计算浮力的浮力的方法，第一个“2”指的是判断浮力大小关系的两种方法、第二个“2”指的是判断物体浮沉的两种方法。

下面，针对这个模型，我会为同学们梳理一下，并利用典型例题，为同学们展示模型的使用方法，明确使用条件。

计算浮力的四种方法

• 示数差法：F浮=G-F示

• 压力差法：F浮=F下-F上

• 公式法：F浮=G排=m排g=ρ液v排g

• 平衡法：F浮=G物体

示数差法：F浮=G-F示

例题：

【解析】

如题，图A测得是合金的重力G=2N；图B测得是合金浸没在水中的弹簧测力计示数 F示=1.5N；则合金浸没的浮力是F浮=G-F示=2N-1.5N=0.5N

压力差法：F浮=F下-F上

例题：

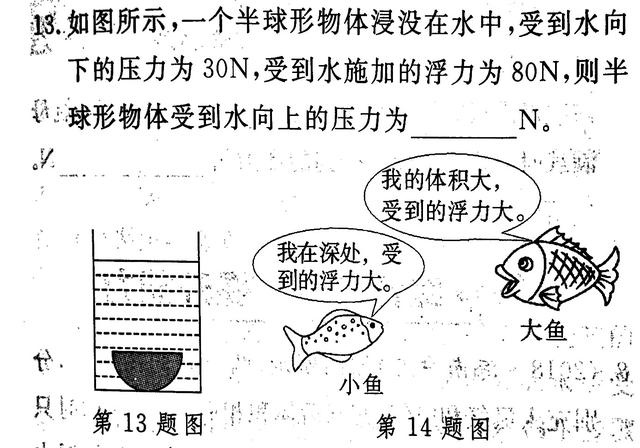
【解析】

如题，条件给了上表面施加在物体上向下的压力 F上=30N，物体受到的浮力 F浮=80N,那么物体下表面受到水施加的向上的压力

F下=F浮+F上=30N+80N=110N

公式法：F浮=G排=m排g=ρ液v排g

例题1：F浮=m排g

【解析】

如题，排出水的质量为 m排=0.2kg，则可以求出物体受到的浮力

F浮=m排g=0.2kg×10N/kg=2N

例题2：F浮=ρ液v排g

【解析】

如题，已知物体的体积是 V物=600cm^3；当物体全部水中的时候，它排出的液体体积等于它自身的体积，即 V排=V物=600cm^3=0.0006m^3。

呢么可以求出物体受到的浮力了，即

F浮=ρ液v排g=1000kg/m^3×0.0006m^3×10N/kg=6N

平衡法：F浮=G物

【解析】

如题，由于木块漂浮在水面上，则有 F浮=G物 的结论，且根据阿基米德原理可以知道 F浮=G排=0.4N。则知道木块的重力G=0.4N

比较物体浮力大小的两种方法

• 公式法：F浮=G排=m排g=ρ液v排g

• 受力分析法：状态决定受力

• 例题1：

【解析】

如题，铅球、铜球、木块的体积相同，且他们都浸没在水中，根据公式

F浮=ρ液v排g 可知，三者受到的浮力大小相等。

例题2:

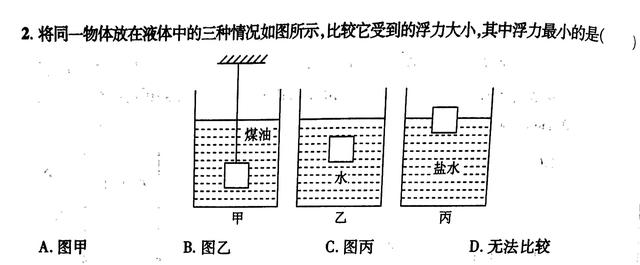
【解析】

如题，由于物体浸在液体中的体积不同（丙与甲乙不同），且三种液体的密度不同，使公式 F浮=ρ液v排g 出现了两个变量，不能讨论，所以要果断放弃这种方法，改用受力分析的方法。

即：

• 甲图中，物体受到了三个力：绳子的拉力、重力、浮力，他们的关系是

• F拉+F浮=G，可知 F浮力<G物

• 乙图中，物体炫富在水中，可知 F浮=G物

• 丙图中，物体漂浮在盐水上，也有F浮=G物

从上面的关系可知浮力最小的是甲图。

判断物体浮沉的两种方法

• 比较密度【ρ液与ρ物的关系】

• 比较受力【F浮与G物的关系】

例题1：比较受力

【解析】

如题，已知物体的质量m=120g，就可以求出物体的重力G=mg=0.12kg×10N/kg=1.2N

又知道排除液体的体积 V排=100cm^3=0.0001m^3，则可以求出浮力

F浮=ρ液v排g=1000kg/m^3×0.0001m^3×10N/kg=1N

这里 F浮<G物，那么物体将沉在溢水杯底部

例题2：比较密度

【解析】

如题，已知物体的体积V=0.002m^3，物体的重力12N，则可以求出物体的质量

m=G/g=12N÷10N/kg=1.2kg。

利用重力和体积，我们就可以求出物体的密度

ρ=m/v=1.2kg÷0.002m^3=600kg/m^3 < ρ水，那么物体将漂浮在水面上，此时

F浮=G物=12N

综合题型

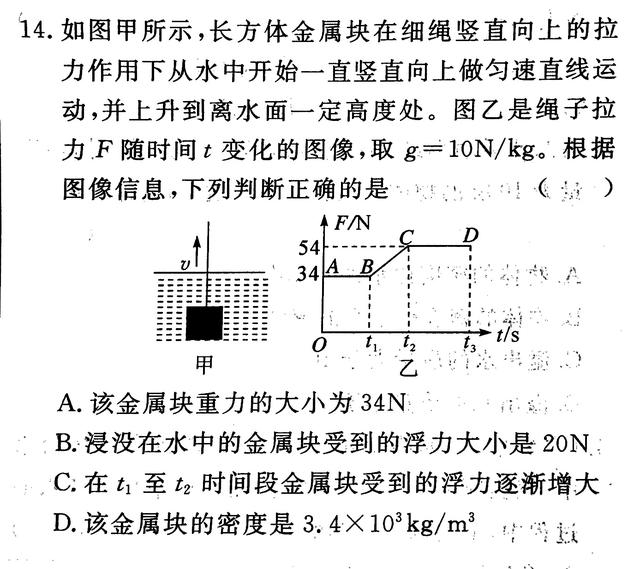
【解析】

如题，物体从底部升起，在没有离开水中的时候，物体的浮力不会变化，所以绳子的拉力在 0–t1 阶段没有发生变化。

自物体上表面碰到水面，到问题下表面离开水面，物体浸在水中体积逐渐减小，受到的浮力逐渐减小，则绳子的拉力逐渐增大，所以C答案错误。（F示=G-F浮）

当物体离开水面之后，绳子的拉力等于物体的重力（匀速直线运动，二力平衡）

从上述分析可知

G=54N，所以A答案错误。

F浮=54N-34N=20N，所以B答案正确。（示数差法：F浮=G-F示）

D答案如下：