开篇语：

最值问题是圆锥曲线的典型问题。是高中数学的重点内容，也是高考的热点。

解决这类问题不仅要牢牢把握圆锥曲线的定义，同时要综合运用代数，平面几何

三角函数等知识，下面是6种题型。希望大家看完后能有所收获！

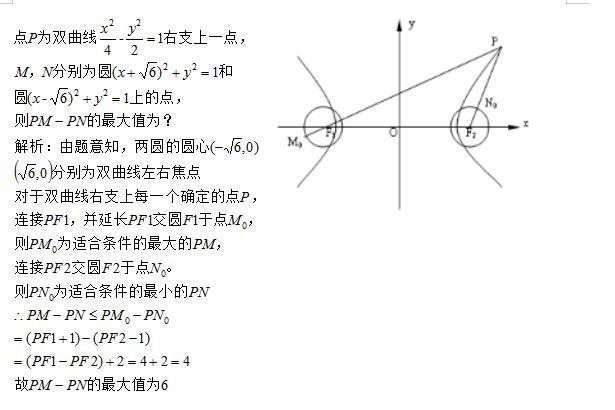
题型一：圆锥曲线和圆的结合

方法：利用圆外一点到圆的距离的最值解题

最大值=圆外点到圆心距离+圆半径

最小值=圆外点到圆心距离-圆半径

题型二：求距离的最值

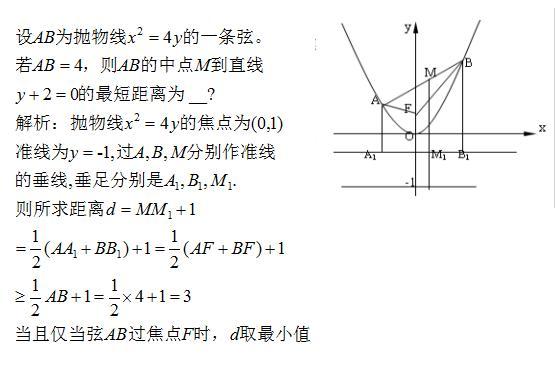
方法：利用抛物线第二定义

抛物线上的点到焦点距离等于到准线距离

抛物线弦长中焦点弦最短

题型三：求角的最值

利用夹角公式，通过斜率的最值判断夹角的最值

题型四：求两条线段长度和最值

方法：利用椭圆第一第二定义，离心率的定义

当三点共线时两条线段长度和最小

题型五：求向量数量积最值

方法：直线和曲线方程联立方程组

解关于直线斜率k的不等式

题型六：求多边形面积的最值

方法：直线和曲线方程联立方程组

解关于直线斜率k的不等式

当不等式比较复杂时

用换元法简便解题

圆锥曲线最值和范围问题常用以下方法解决：

(1)结合定义，利用图形中几何量之间的大小关系

(2)不等式求解法：利用题意结合图形，列出所讨论的参数适合的不等式，通过解不等式组得到参数的变化范围

(3)函数值域求解法：把所讨论的参数当做一个函数的自变量，通过讨论函数的值域来求出参数的变化范围

(4)利用基本不等式：基本不等式的运用，常常需要创造条件，进行巧妙的构思，辅以解不等式常用的方法快熟解题

总结：圆锥曲线选择填空的最值题目，主要是利用曲线的第二定义，将代数问题转化为几何问题，利用三点共线，或者三角形两边和大于第三边，两边差小于第三边等知识巧妙解题

大题主要是联立方程解关于某个参数的不等式。