二次函数配方口诀

求二次函数y=ax2+bx+c的顶点坐标、对称轴方程、最大值或最小值等都需要运用配方法将二次函数化为y=a(x-h)2+k的形式，其中配方是学习中的难点，这里的配方虽然与一元二次方程的配方有点类似，但不尽相同，不少初学者茫然无措．现将配方过程归纳为如下口诀，方便大家的学习．

二次系数先提取，常数暂且往后移；

一次系数取一半，平方以后再加减；

前三配方四相乘，最后再算常数项．

口诀解析：

"二次系数先提取，常数暂且往后移"的意思是：

把y=ax2+bx+c的二次项系数a作为公因式提取，常数项c放到括号外的后面，化为：

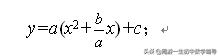
"一次系数取一半，平方以后再加减"的意思是：

在括号内的x2+bx/a，取一次项的系数b/a的一半b/(2a)，加上和减去它的平方[b/(2a)]2，化为：

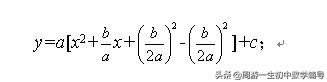
"前三配方四相乘"的意思是：

具体运用看如下例子：

例1 把y=2x2-3x-5化为y=a(x-h)2+k的形式.

解："二次系数先提取，常数暂且往后移"，得：

y=2(x2-3x/2)-5；

"一次系数取一半，平方以后再加减"得：

y=2(x2-3x/2+9/16-9/16)-5；

"前三配方后相乘"，得

y=2(x-3/2)2-9/16×2-5；

"再加后面常数项"，得：

y=2(x-3/2)2-49/8.

例2 用配方法求二次函数y=-x2+4x+1的图象顶点坐标．

解：根据配方口诀，得：

y=-( x2-4x)+1

=-( x2-4x+4-4)+1

=-[ (x-2)2-4]+1

=-(x-2)2-4×(-1)+1

=-(x-2)2+5.

所以顶点坐标为（2，5）．

例3 求二次函数y=3x2/2+9x-7的最小值．

解：根据配方口诀，得：

y=3/2(x2+6x)-7

=3/2(x2+6x+9-9)-7

=3/2[(x+3)2-9]-7

=3/2(x+3)2-9×3/2-7

=3/2(x+3)2-41/2，

因为a=3/2>0，所以当x=-3时，y最小值=-41/2.

例4 求抛物线y=ax2-4ax+1的对称轴方程．

解：y=a(x2-4x)+1

=a(x2-4x+4-4)+1

=a[(x-2)2-4]+1

=a(x-2)2-4a+1，

所以对称轴方程为x=2.