中考数学经典几何模型：最值

类型一 “将军饮马”模型

通过对称进行等量代换，转化成两点之间的距离或点到直线的距离，或利用三角形两边之和大于第三边，两边之差小于第三边求得最值。

1、同侧、异侧两线段之和最短

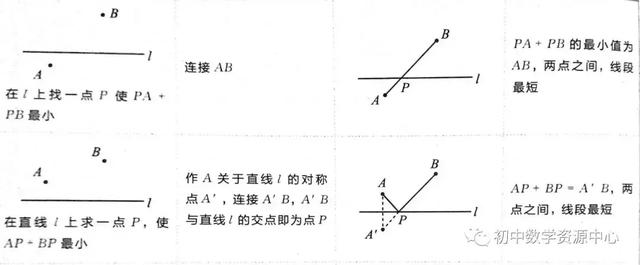
2、同侧、异侧两线段之差最大、最小

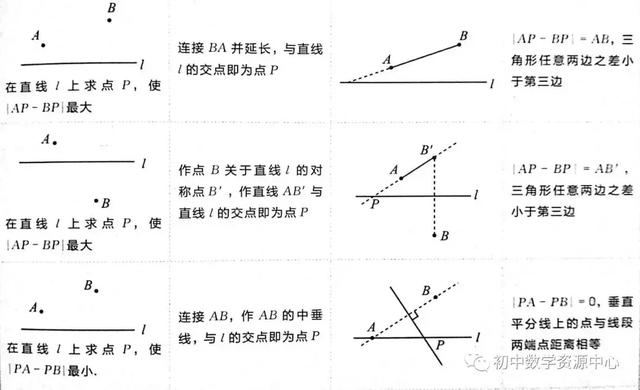
例1：已知A. B. C. D四点如图所示，请画出一点P，使P到点A. B. C. D的距离之和最小，并说明理由。

简答：连接AD、BC,令其交点为P,在线段BC上任取一点Q(不同于点P)，连接AQ、DQ，如图所示。

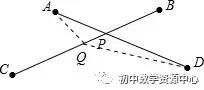
∵点P，点Q均在线段BC上，

∴PB+PC=QB+QC，

∵点P在线段AD上，

∴PA+PD=AD，

在△QAD中,QA+QD>AD(两边之和大于第三边)，

即QA+QB+QC+QD>PA+PB+PC+PD.

∴线段AD、BC的交点P为所要找的点。

例2：如图：A，B两点在直线的两侧，点A到直线的距离AM=4，点B到直线的距离BN=2，且MN=4，P为直线上的动点，PA+PB的最小值为 ，|PA−PB|的最大值为 ，|PA−PB|的最小值为 。

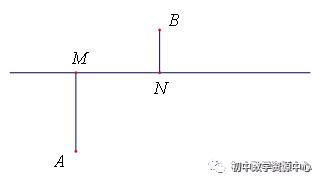
简答：（1）连接AB，交MN于点P，此时PA+PB最小=2√13

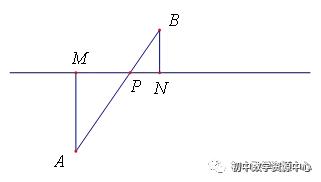
（2）作B点关于MN的对称点B′，连接AB′并延长，与直线MN交于点P，此时|PA−PB|的值最大=PA-PB′=AB′=2√5

理由：在直线MN上任找异于点P的一点P′，连接P′A，P′B′

由三角形两边之差小于第三边可知，P′A-P′B≤AB′，当A、B′、P′三点共线时，取得最值

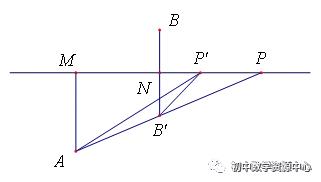
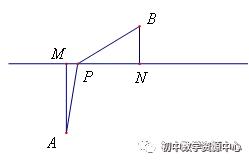
（3）易知：在直线MN上存在一点P，使得PA=PB，此时|PA−PB|的值最小为0

3、三角形、四边形周长最小

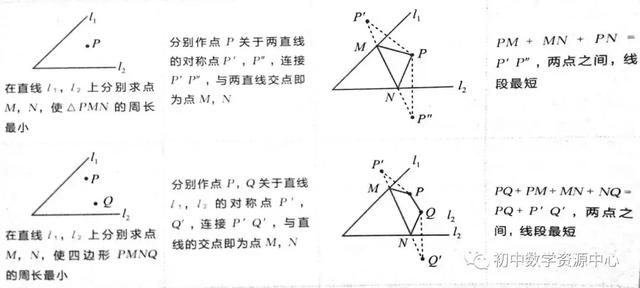
例1：如图,在四边形ABCD中,∠BAD=110∘,∠B=∠D=90∘.在BC，CD上分别找一点M，N，使△AMN周长最小，则∠AMN+∠ANM的度数为 .

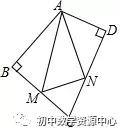
解答：

如图,作点A关于BC的对称点A′，关于CD的对称点A″，

连接A′A″与BC、CD的交点即为所求的点M、N,

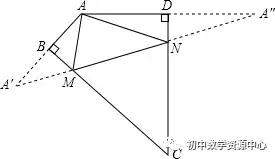
∵∠BAD=110∘,∠B=∠D=90°，

∴∠A′+∠A″=180°−110°=70°，

由轴对称的性质得：∠A′=∠A′AM，∠A″=∠A″AN，

∴∠AMN+∠ANM=2(∠A′+∠A″)=2×70°=140°.

例2：如图,∠MON=20°,A、B分别为射线OM、ON上两定点,且OA=2,OB=4,点P、Q分别为射线OM、ON两动点,当P、Q运动时,线段AQ+PQ+PB的最小值是

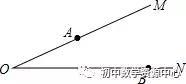
解答：

作A关于ON的对称点A′,点B关于OM的对称点B′,连接A′B′,交于OM,ON分别为P,Q,连接OA′,OB′，

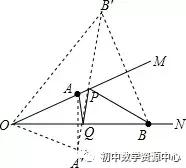
则PB′=PB,AQ=A′Q,OA′=OA=2,OB′=OB=4,∠MOB′=∠NOA′=∠MON=20°，

∴AQ+PQ+PB=A′Q+PQ+PB′=A′B′,∠A′OB′=60°，

∵cos60°=1/2,OA′/OB′=1/2，

∴∠OA′B′=90°，

∴A′B′=2√3，

∴线段AQ+PQ+PB的最小值是：2√3.

4、需要平移的“将军饮马”

例题：如图，已知四边形ABCD四个顶点的坐标为A(1,3)，B(m,0)，C(m+2,0)，D(5,1)，当四边形ABCD的周长最小时，m的值为______.

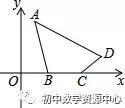
解答：

将C点向左平移2单位与B重合,点D向左平移2单位到D′(3,1)，

作D′关于x轴的对称点D″，则点D″(3,−1)，

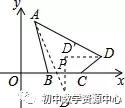
设直线AD″的解析式为y=kx+b，

带入A、D″两点坐标，解得k=−2，b=5.

∴直线AD″的解析式为y=−2x+5.

当y=0时,x=5/2，

即B(5/2,0),∴m=5/2.

5、点到直线垂线段最短

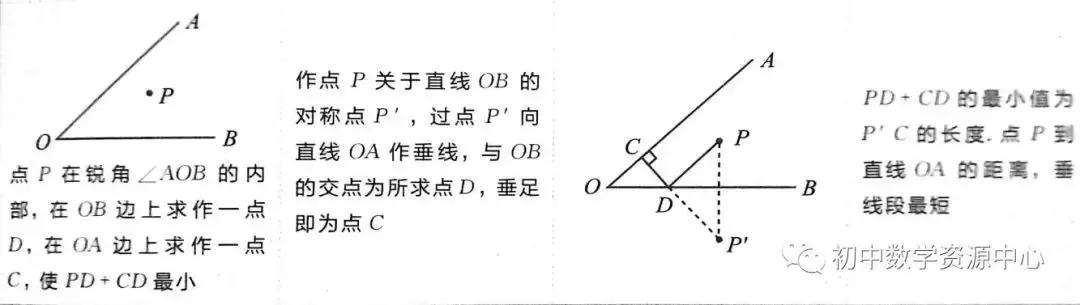
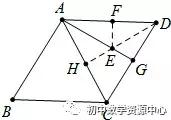
例1：如图,在菱形ABCD中,AB=6,∠B=60∘，点G是边CD边的中点，点E. F分别是AG、AD上的两个动点，则EF+ED的最小值是 .

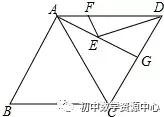
解答：

如图作DH⊥AC垂足为H与AG交于点E，

∵四边形ABCD是菱形，

∵AB=AD=CD=BC=6，

∵∠B=60°,

∴∠ADC=∠B=60°，

∴△ADC是等边三角形，

∵AG是中线，

∴∠GAD=∠GAC

∴点H关于AG的对称点F在AD上，此时EF+ED最小=DH.

∴EF+DE的最小值=DH=3√3

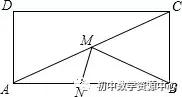
例2：如图,矩形ABCD中,AD=5,AB=12,点M在AC上,点N在AB上,则BM+MN的最小值为( )

简答：

作B点关于AC的对称点E点，过E作EF垂直AB交AB于F点，

AC=13，

AC边上的高为60/13,所以BE=120/13.

∵△ABC∽△BEF，

∴AB/EF=AC/BE，

求得EF=1440/169.

类型二 由已知定长线段求最值

找到与所求最值相关成三角形的两个定长线段，定长线段的和为最大值，定长线段的差为最小值。

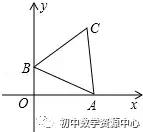
例1、如图，边长为10的等边△ABC的顶点A，B分别在x轴正半轴和y轴正半轴上运动，则动点C到原点O的距离的最大值是 。

简答：

如图，取AB中点P，连接OP、PC，

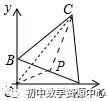
CP、OP长都是定值，CP=5√3，OP=5

∵OP+PC ≥ OC，

∴当O、P、C共线时,OC的值最大,最大值=5+5√3.

例2、如图，在RT△ABC中，∠ABC=90°，AB=4，BC=3，点D是半径为2的圆A上的一个动点，点E是CD的中点，则BE长的最大值是多少？

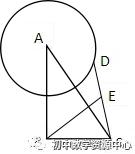
简答：如图，取AC的中点F，连接BF、EF、AD

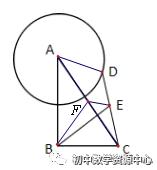
AD=2，EF是△ACD的中位线，∴EF=1，是定值

BF是RT△ABC斜边上的中线，∴BF=1/2AC=5/2

∴BE≤BF+EF=1+5/2=7/2

B/F/E三点共线时BE取得最大值

类型三 旋转最值模型

通过旋转，找到与所求最值相关成三角形的两个定长线段，定长线段的和为最大值，定长线段的差为最小值。

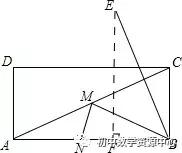
例1、如图，四边形ABCD中，AB=4，BC=3，△ACD为等边三角形，求BD的最大值。

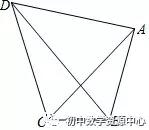
简答：将△ABD绕D点顺时针旋转60°，DA与DC重合，DB到DE的位置

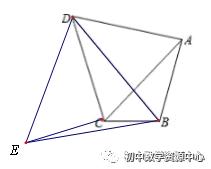
易证△DEB为等边三角形，BC=3，EC=AB=4，均为定值

∴BD=BE≤BC+EC=7

当B、C、E三点共线时取得最大值

2、在正方形ABCD外有一点P，PA=3，PB=4，AC，BD交于O点，求OP的最大值

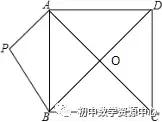
简答：连接OP，将△AOP绕O点旋转90°至△OBP′处，连接BP′、PP′

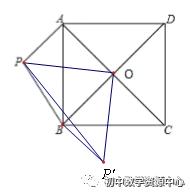
可知△OPP′为等腰直角三角形，∴OP=√2/2PP′

已知BP=4，BP′=AP=3，均为定值

∴PP′≤BP+BP′=7

∴PP′的最大值为7

∴OP的最大值为7√2/2