开篇语：

参数方程作为新课标的选修内容，知识点不多，题型难度也不大，属于必须掌握的内容。

主要内容是参数t的几何意义，直线，圆，圆锥曲线等对应的参数方程

3种题型：

1，参数方程与普通方程的互化

2，参数t的应用

3，参数方程与极坐标方程的综合

重点：直线的参数方程中，参数t的系数的平方和为1时，t才有几何意义且其几何意义为：|t|是直线上任一点M(x，y)到M₀(x₀，y₀)的距离，即|M₀M|＝|t|.

题型一：参数方程与普通方程的转化

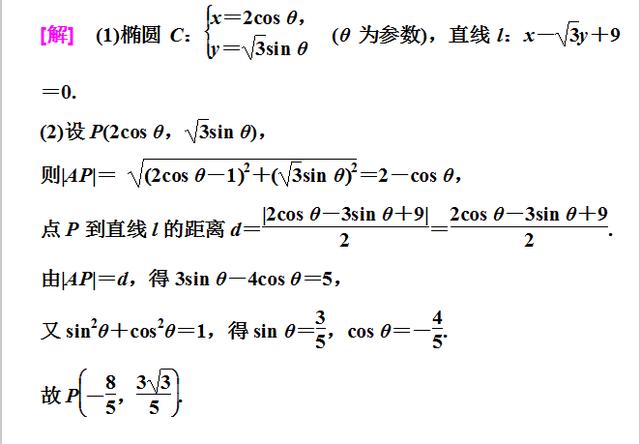
将参数方程化为普通方程的方法

(1)将参数方程化为普通方程，需要根据参数方程的结构特征，选取适当的消参方法．常见的消参方法有：代入消参法、加减消参法、平方消参法等，对于含三角函数的参数方程，常利用同角三角函数关系式消参，如sin²θ＋cos²θ＝1等．

(2)将参数方程化为普通方程时，要注意两种方程的等价性，不要增解．

题型二：参数t的应用

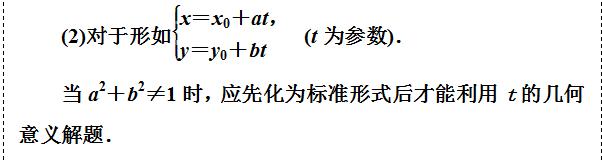
题型三：参数方程和极坐标方程综合

处理极坐标、参数方程综合问题的方法

(1)涉及参数方程和极坐标方程的综合题，求解的一般方法是分别化为普通方程和直角坐标方程后求解．当然，还要结合题目本身特点，确定选择何种方程．

(2)数形结合的应用，即充分利用参数方程中参数的几何意义，或者利用ρ和θ的几何意义，直接求解，能达到化繁为简的解题目的．