解题新思路：
探究数学问题解决的新思路，对于学生发散性思维和创造性思维的培养是十分有利的。下面一道例题，是从多维度角度出发来探究解题新思路的
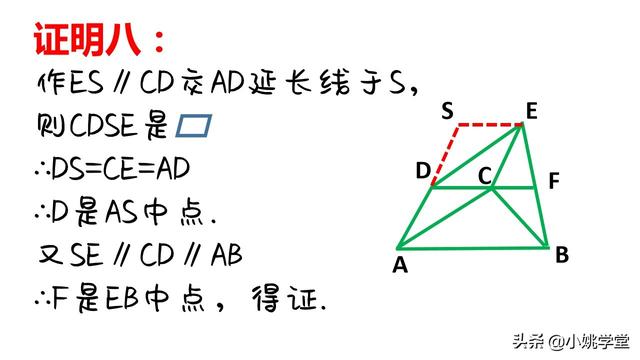
总之，上述不同证法的辅助线可归结为以下两种：
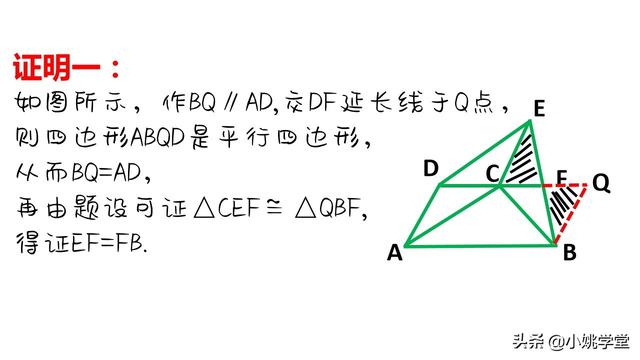
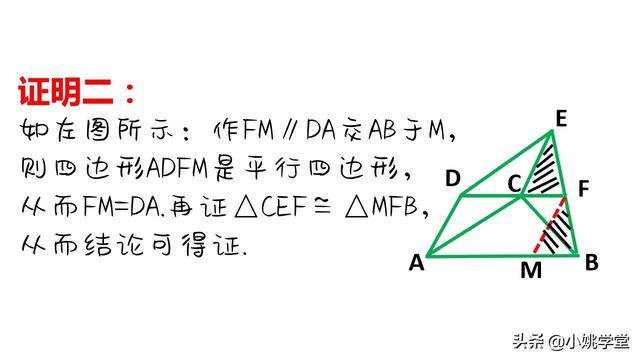
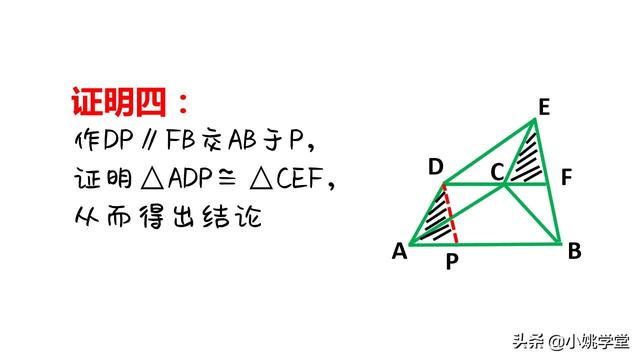
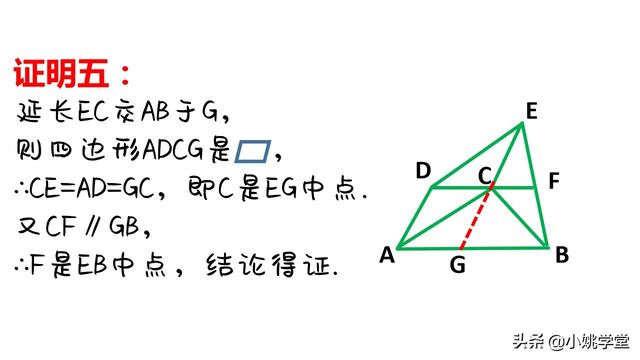
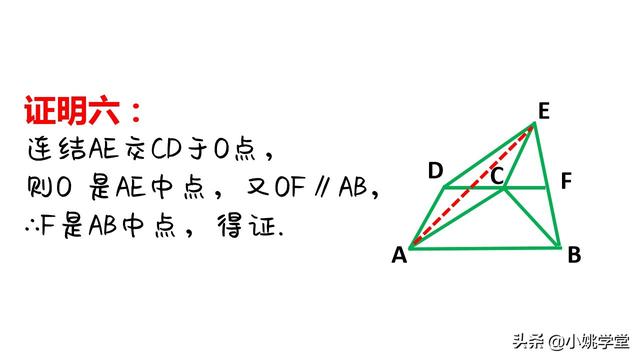
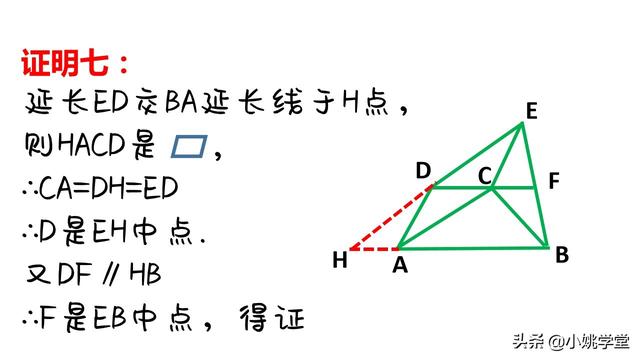
①作平行线构成平行四边形和全等三角形进行等量代换。
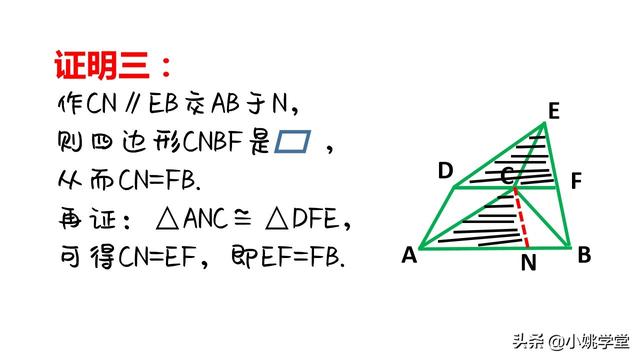
②作平行线，由题设产生中点，通过平行线等分线段定理的推论得出结论。
这其中，其实蕴含了平面几何的平移变换和旋转变换的数学思想。
上一篇 : 九年级第二学期学业数学试卷
下一篇 : 初中几何你不得不知的十大模型，轻松解决几何难题
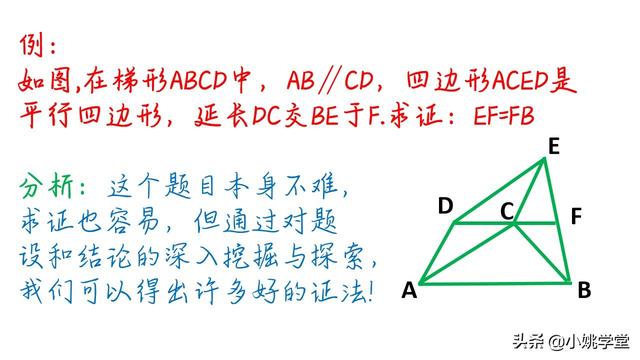
初中数学，一题八解，求证：EF=FB，多维度角度来探究解题新思路
解题新思路：
探究数学问题解决的新思路，对于学生发散性思维和创造性思维的培养是十分有利的。下面一道例题，是从多维度角度出发来探究解题新思路的
总之，上述不同证法的辅助线可归结为以下两种：
①作平行线构成平行四边形和全等三角形进行等量代换。
②作平行线，由题设产生中点，通过平行线等分线段定理的推论得出结论。
这其中，其实蕴含了平面几何的平移变换和旋转变换的数学思想。
上一篇 : 九年级第二学期学业数学试卷
下一篇 : 初中几何你不得不知的十大模型，轻松解决几何难题
初中数学，“将军饮马”的七大模型
人教版八年级数学上册第一章单元测试题（含答案）
初二《全等三角形》数学模型之“一线三等角”模型
加载中,请稍侯......
精彩评论