初中数学 “捆绑”在解题中的妙用

1：

1

第一空比较简单，我们不作研究，重点在第二空，你怎么看？找规律当然是通法，计算量有些大。

接下来我们换一个角度思考。∆AB₁C₁可看作∆ABC关于点A作位似变换，下面将∆ABC与内接正方形捆绑，那么两个正方形其实也是作位似变换，且相似比与三角形一致。三角形的相似比是底边B₁C₁：BC，而正方形的相似比是边长B₂C₂：B₁C₁，而这个比恰恰又是下一对三角形的底边之比，换而言之，相邻两正方形的相似比为定值。接下来B_nC_n便能呼之欲出了。

小结：将三角形与其内接正方形捆绑，找共性。

2：

2

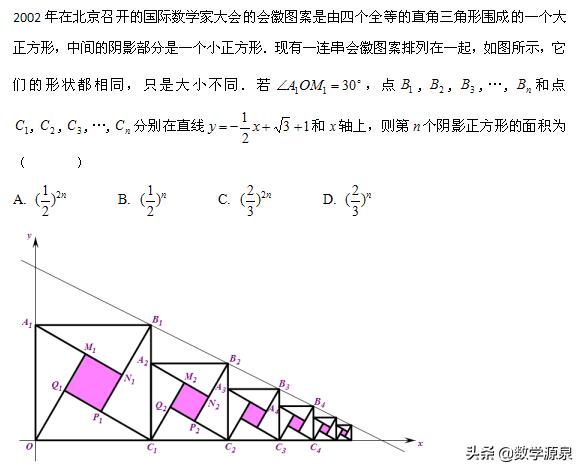
这道题的解析也是不断计算各个面积，找规律。其实容易发现相邻两个正方形的比值是定值。现在将阴影部分与正方形捆绑，那么阴影部分的相似比也是这个定值。等比数列已知首项和公比就能表示通项。

例1：

例1

嘉兴这几年连续在填空压轴位置放路径问题，就如重庆喜欢正方形，天津喜欢作图，哈尔滨喜欢圆压轴，可惜今年嘉兴中考放弃了这个坚持。

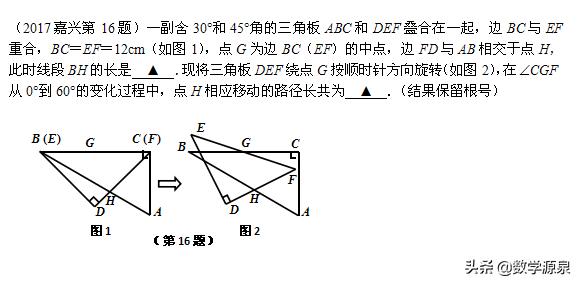
第一题确定性分析：∠HBC定，∠BCH定，BC定，则∆BCH定，BH可求。接下来解三角形即可。

本道题第二空的难点在于对点H运动路径的判断，这甚至让很多老师无从下手，我还是看到许多老师最后借助几何画板……有一点很清楚，学生考试是不能用几何画板的。

网上还有一些解法，以构造为主，或许讲了学生能懂，再做还是困难重重的。

我的想法是怎样思考比较自然？即使要用辅助线也是自然生成。我在群里发过一次解法，当时也有老师问起怎么想到的，所以趁这个机会和大家一起交流。

首先确定性分析。这个意识老师和学生都要有，任何几何动态问题首先要进

行确定性分析。点H是AB和DF的交点，AB定，DF动。于是目光就要转向DF，

显然DF绕点G做逆时针旋转。那么它的运动有着怎样的规律？

对于一条直线的定位一般有两种方法：（1）两点法；（2）点角法

这里用点角法很容易作出下面的图形：

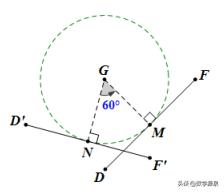
接下来将DF与圆G捆绑，则DF为弧MN上的动切线。还有一个细节，考虑两点法，点F的对应点F’必定落在AB上，这是一个特殊位置应当关注。

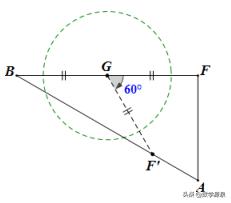
再来看整张图：

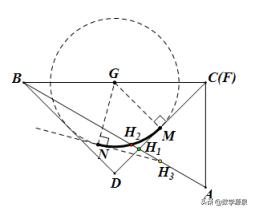
H是AB和DF的交点，DF为弧MN上的动切线，

关键点1：初始状态，DF与圆的切点为M，此时AB和DF的交点为H1

关键点2：DF绕点G旋转，交点H向AB方向移动，逐步达到圆与AB的交点H2

关键点3：DF继续绕点G旋转，交点H向BA方向移动，终止状态，DF与圆的切点为N，此时AB和DF的交点为H3，即H由H1（CD与AB的交点）到H2（⊙G与AB的交点）再到H3（点N处切线与AB的交点），大家看，H的路径非常自然地“现行”了。接下来只需解三角形就能解决

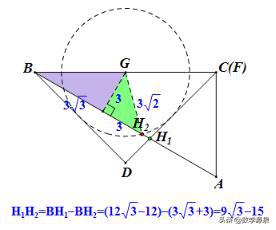
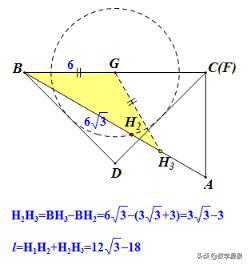
回顾一下刚才的想法，捆绑是手段，而核心是图形的确定性。

于特也说过“几何构造很美妙，几何构造伤不起”，学生不易掌握。上述所用的方法从确定性入手，思维过程比较自然，当然关键还是在于教师平时课堂有没有引导学生进行确定性分析，而不是某一道题目突然抛出。

上题可以称为直线型来回路径

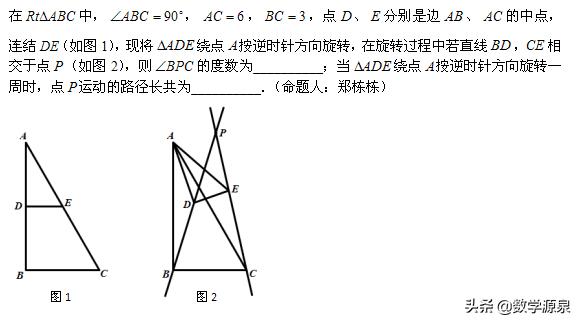
例

第一空比较简单，当时的设计也是为第二空做铺垫。手拉手模型易得∆ABD~∆ACE，则有∠BPC=30°

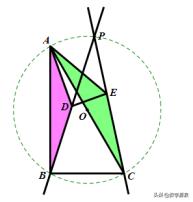
第一空更为重要的是带来了点P的轨迹这一“战利品”：以AC中点O为圆心3为半径的圆。

第二空还是先确定性分析。点P如何产生？BD和CE的交点，但是这两条线都在动，怎么办？

第一题带来了春天，P亦可看作BD和圆O的交点，BD动，圆O定，接下来研究BD。

B是定点，D是动点，D怎么动？D在以A为圆心AD为半径的定圆上运动！于是将BD与圆A捆绑，BD是圆A的动割线（或切线）

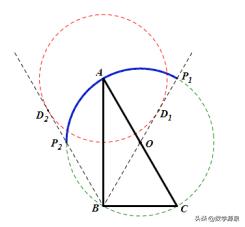
关键点1：P从A（起点）出发，按顺时针方向旋转

关键点2：当BD与圆A相切（右）时，P达到第一个极端位置P₁

关键点3：P从P₁按逆时针方向旋转，当BD与圆A相切（左）时，P达到第二个极端位置P₂

关键点4：P从P₂按顺时针方向旋转，回到点A（终点）

计算就容易了，易得∠ABP₁=30°，L=4π.

本道题的命题意图当时也写了一下，和大家分享：

本题以特殊三角形中位线为背景，似曾相识，由易到难，要求学生经历分析、猜想、探究、证明、计算等过程，对学生的几何思维能力要求较高．题目融合图形旋转、直角三角形、中位线、相似三角形、圆、三角函数等初中几何领域核心知识，考查了学生综合运用知识、作图探究、分析问题、简化问题的能力。

下面再来一道2017浙江地区的压轴解答题，这道题十分漂亮，大家先看看，今天解决的是第（3）小问：

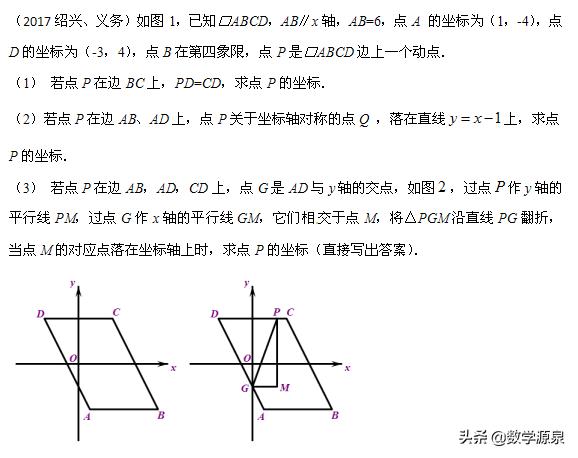
例

下面来探讨第（3）问的解法。这个问题首先会涉及两处分类：（1）点P在CD，AD，AB三个位置；（2）M的对应点M’可以落在x轴与y轴上。

情况一：当P在CD上时，先定性分析：若M’落在y轴上，四边形M’GMP必为正方形，PM=6，GM<6，这里用“边”很容易判断是不可能的。

而落在x轴上直观判断是可行的。如果可行点M如何定位？

接下来确定性分析。G是定点，P、M是动点，那么M运动有何规律？

不难发现M的对应点M’落在x轴上，它的轨迹是一条直线，于是将M’与x轴捆绑，翻折回来得到点M的轨迹必然也是直线。于特喜欢把它称作“反手勾拳”。

下面我们来探讨如何定位这条直线

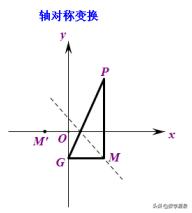
很显然点M所在的直线是把x轴作关于PG的轴对称变换得到，但是PG的定位有一定的难度，况且问题本身就是要求P的坐标，凭直觉不是明智之举。那怎么办？

乾坤大挪移。思维转化。

点P不定，但点G是定点。于是我们不妨将直线看作是由x轴绕点G顺时针旋转2∠OGP的度数得到。把轴对称转化为旋转，其效果是等价的。而我们只需要解决∠OGP的度数便能顺利对直线定位。

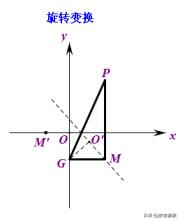
所以我们就研究其中一个图形即可：

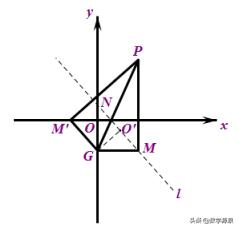
下面介绍几种方法：

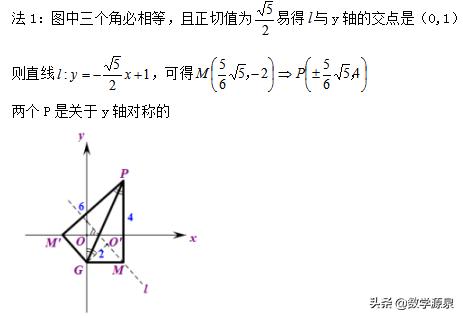
方法1

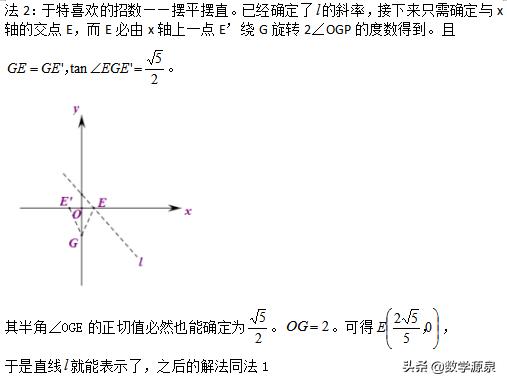
方法2

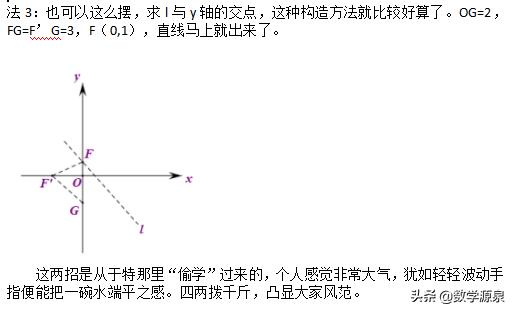
方法3

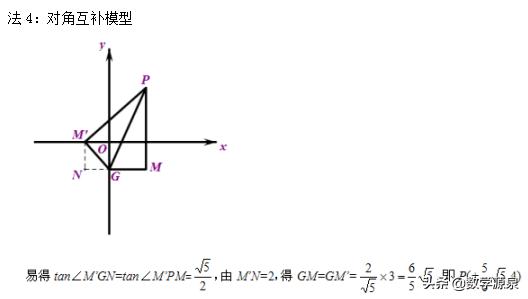
方法4

情况二：当P在AD上时，k_PG=k_AD=－2，四边形M’GMP不可能为正方形，故M’不可能落在y轴上。之前的情况用边来判断是否为正方形，这里用的是角，比较方便，而上一种情况用边来判断，题目很美妙。

继续分析，当P在GA上时显然M’不可能落在x轴上，而当P在DG上时有可能使M’落在x轴上．

接下来的思考方式仍与之前一样，仍然可以确定性分析，即用旋转来代替轴对称。这种情况的数据也很有意思，tan∠M'PG=tan∠MPG=1/2.熟悉12345的话直接口算了。

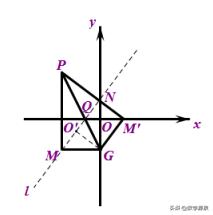
前面提到的四种方法都可以用，相对来说对角互补比较易算。

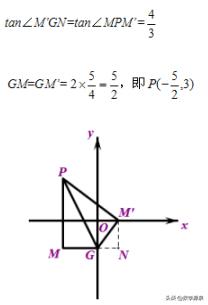
情况三：当P在AB上时，显然M’不可能落在x轴上，有可能使M’落在y轴上．易得四边形M’GMP是正方形，此时P（2，－4)

下面是最后一道题：

例

我们着重研究第（3）题，这一小题当时的评分标准如下：

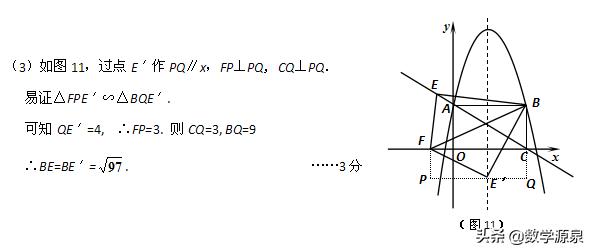
评分标准里的答案非常简化，以致于这道题的得分率是比较高的。在很多学生都能做对的情况下，我有两个疑惑：

（1）当E在直线AC上移动时，BE：EF的比值是否改变？

（2）对称点E’的个数为何只有一个？

学生虽然做对了，但是这两个疑惑，尤其是第二个，学生真的明白？

下面由我的一位学生来回答这两个问题，当时我在课堂点出了疑惑，学生当场解决（这位学生二模考了满分，被嘉兴最顶尖的高中提前录取），下面我把学生的解释还原。

解答一：当E在直线AC上移动时，BE：EF的比值是否改变？

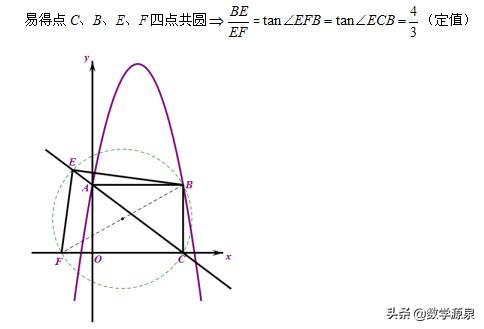
解答二：对称点E’的个数为何只有一个？

将E’与对称轴捆绑，点E是由点E’绕点B顺时针旋转正切值为24/7的角度（∠MBN）得到，将对称轴绕点B顺时针旋转正切值为24/7的角度得到直线

，则点E必在直线L上．而点E又在直线AC上，故点E唯一确定．

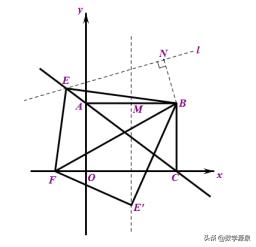
这里的24/7是这么得到的（矩形大法）：

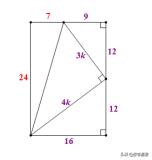
这两个半倍角组合很美妙：

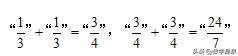
命题老师看到这个数据一定会有所联想

最后这个问题的解决并不难。只需构造K型图即可。

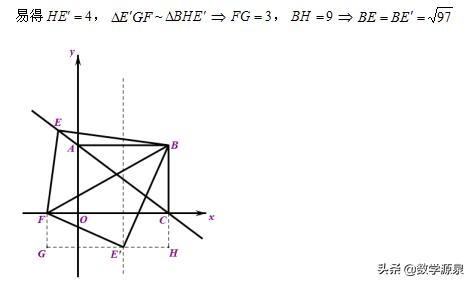
但是答案背后隐藏的东西却值得深思。

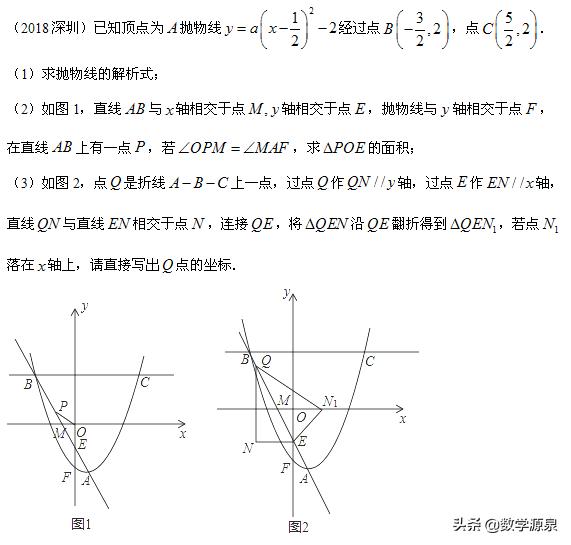
这种类型的翻折问题近几年似乎比较流行，2018年深圳的压轴解答题也考了类似的问题，最后两问都可以用捆绑解决，如果再配合12345、矩形大法、增量巧设这些绝招就可以“一路顺风”了。有兴趣的老师可以去做做。