中考热点题型：内外角平分线与角相关解题思想

考情分析

三角形内外角平分线的的概念是处理与角相关问题的基本依据和方法，在中考题中经常利用角平分线的性质去证明角或者线段的相等，三角形的全等。最近几年题型出现创新性变化，比如利用角平分线的对称性把图形翻折，再进行推理计算。形式变了，解题思想的精髓还在。

角平分线四大基本题型分析

已知P是∠MON平分线上的一点，

1.若PA⊥OM于点A，如下图所示，可以过点P作PB⊥ON于点B，则PB=PA。

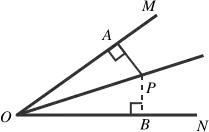
图中有角平分线，可以向两边作垂线。

2.若点B是射线ON上任意一点，如下图所示，可以在OM上截取OA=OB，连接PA，构造△OPA≌△OPB。

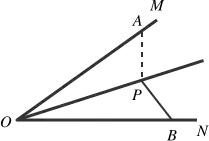
图中有角平分线，以角平分线为对称轴，构造全等三角形。

3.若AP⊥OP于点P，如图c所示，可以延长AP交ON于点B，构造△AOB是等腰三角形。P是底边AB的中点。

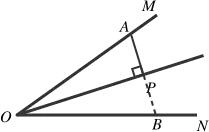
有角平分线有垂线，可试找三线合一。

4.过点P作PQ∥ON交OM于点Q，如下图所示，可以构造△POQ是等腰三角形。

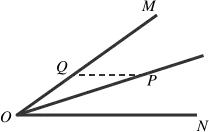
有角平分线和平行线，构造等腰三角形得出更多的边角关系。

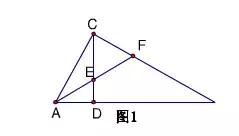
如图1，RT△ABC中，∠ABC=90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CD于点F。

（1）求证：CE=CF。

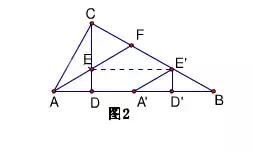
（2）将图1中的△ADE沿AB向右平移到△A'D'E'的位置，使点E'落在BC边上，其它条件不变，如图2所示，试猜BE'与CF有怎样的数量关系？证明你的结论。

点拨

第1问主要考察一个模型“双垂直+角平分线”，可得等腰三角形。

第2问遇到角平分线通常考虑过角平分线上一点向角的两边作垂线，所以过点E作AC的垂线，构造全等三角形解题。也可以过点F作AB的垂线。

（1）证明：∵AF平分∠CAB,

∴∠CAF=∠EAD,

∵∠ACB=90°,

∴∠CAF+∠CFA=90°,

∵CD⊥AB于D,

∴∠EAD+AED=90°,

∴∠CFA=∠AED,

∵∠AED=∠CEF,

∴∠CFA=∠CEF,

∴CE=CF；

（2）BE′=CF．

证明：如图,过点E作EG⊥AC于G,

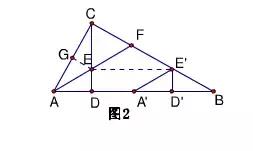
∵AF平分∠CAB,ED⊥AB,

∴ED=EG．

由平移的性质可知：D′E′=DE,

∴D′E′=GE,

∵∠ACB=90°,

∴∠ACD+∠DCB=90°

∵CD⊥AB于D,

∴∠B+∠DCB=90°,

∴∠ACD=∠B,

在Rt△CEG与Rt△BE′D′中,,

∴△CEG≌△BE′D′,

∴CE=BE′,

由（1）可知CE=CF,

∴BE′=CF．

对于涉及角平分线的问题，解题时常需作适当的辅助线，构成等腰三角形，然后运用有关性质来解决。还有就是利用角平分线为角的对称轴这一对称性来求解的，实质上就是对称问题了。

思考

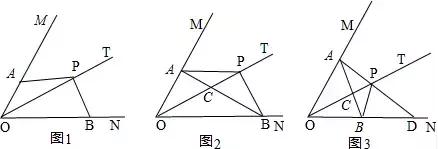
已知，点P是∠MON的平分线上的一动点，射线PA交射线OM于点A，将射线PA绕点P逆时针旋转交射线ON于点B，且使∠APB+∠MON=180°。

（1）利用图1，求证：PA=PB；

（2）如图2，若点C是AB与OP的交点，当S△POB=3S△PCB时，求PB与PC的比值；

（3）若∠MON=60°，OB=2，射线AP交ON于点D，且满足且∠PBD=∠ABO，请借助图3补全图形，并求OP的长。