中考数学提分36计之第7计，解不等式(组)中的难题，数轴大显身手

中考中常常出现已知不等式(组)的解集(或特殊解)求不等式(组)中某些字母的取值范围的问题。 这类问题的解答，对思维有较高的要求，因此常常作为考试的提高题出现。这些不等式(组)是动态的,要研究它就要让它静下来、定下来,把它变成一个确定的不等式(组)来解。借助数轴,利用数形结合思想是行之有效的方法。

1、已知一元一次不等式的解集，求字母系数的值

例1、已知关于x的不等式2x－m＞－3的解集，如图1所示，则m的值为（ ）

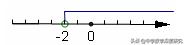
A、2 B、1 C、0 D、－1

分析：从数轴先确定关于x的不等式2x－m＞－3的解集为x＞－2，然后利用不等式和方程的联系或对照解集进行求解。

解：方法一：从数轴上可以看出不等式2x－m＞－3的解集为x＞－2，所以方程2x－m=－3的解是x=－2，故2(－2) －m=－3, m=－1，故选D

方法二：从数轴上可以看出不等式2x－m＞－3的解集为 x＞－2，

又由不等式2x－m＞－3，得x＞（m-3）/2，所以（m-3）/2=－2 ，即m=－1

点评：不等式的解有无数个，但解集是唯一的。

2、已知一元一次不等式的特殊解，求字母系数的取值范围

例2、关于x的不等式-2k-x+6＞0的正整数解只有1、2、3，求正整数k的值。

分析：先确定不等式的解集为x＜-2k+6，然后根据正整数解只有1、2、3，可知-2k+6必须要大于或等于4，且小于5。

解：因为不等式-2k-x+6＞0的解集为x＜-2k+6，再由已知条件：不等式的正整数解只有1、2、3，可知x＜4（但它不一定是不等式的解集），故-2k+6=4，从而求出k=1。

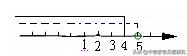
点评：若感觉解答不易理解的话，我们可以利用数轴来确定"-2k+6"的范围，即如图2。这种数形结合的方法值得同学们重视。化动为静巧解含参不等式(组),即把关键之值(不等式中等号成立的情况)代入题中来验证是否满足条件是这类问题常用策略.

3、已知一次不等式组的解集，求字母系数的取值范围

点评：（1）将所面临的问题转化为方程问题；（2）解这个方程或讨论这个方程，得出相关的结论；（3）将所得出的结论再返回到原问题中去.

点评：确定不等式组中字母的取值范围常用方法有下列四种①逆用不等式组解集确定；②分类讨论确定；③从反面求解确定；④借助数轴确定．

A.3 B.1 C.－1 D.－3

分析：因为m的值不确定，所以2m+1与m+2的大小无法比较，因此需从解集为x>－1入手将原题进行分类讨论.

解：若2m+1= －1，即m=－1时，m+2=1，这时不等式组的解集是x>1，与题设矛盾，故m≠－1；若m+2=－1，即m=－3时，2m+1=－5，这时不等式组的解集是x>－1，与题设相符，因此m=－3，故应选D.

点评：当问题存在多种不同情况时，要特别注意分类加以讨论，否则易出错而漏接.

4、已知一次不等式组的特殊解，求字母系数的取值范围

点评：已知不等式组的解集，求所含字母系数的取值（或取值范围），是确定不等式组的解集方法的逆向运用．处理这类问题时，可先求出原不等式组含有某些字母的解集，然后对照已知，采取针对性的方法来解决．

5、考查用不等式(组)解决方程问题

例6、已知2a－3x＋1＝0，3b－2x－16＝0，且a≤4＜b，求x的取值范围．

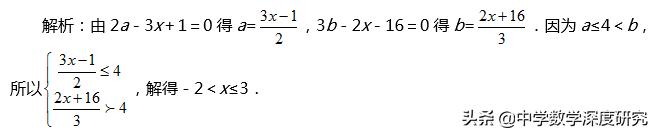
点评：方程与不等式是紧密联系的，很多情况下它们可以相互渗透，利用不等式（组）可以解决方程（组）的问题，反过来也可以利用方程（组）解决不等式（组）问题．

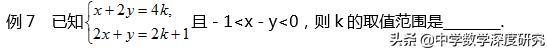
解：将方程组中的两个方程组相减，得x－y=－2k+1.将其整体代入－1<x+y<0，得－1<－2k+1<0.解不等式组，得1/2<k<1.

点评：本题在求解过程中，两次运用了整体思想，一次是将方程组中的两个方程相减；一次是将－2k+1整体代入，这样比求出方程组的解后再代入要简捷.在解决类似问题时，应注意整体思想的灵魂运用.

6、用不等式解决实际问题中的参数值

例8．（2018秋•大连期末）"绿水青山就是金山银山"，高新区凌水河治理工程正式启动，若由甲工程队单独完成需10个月；若由甲、乙两工程队合做4个月后，剩下工程由乙工程队再做5个月可以完成．

（1）乙工程队单独完成这项工程需几个月的时间？

（2）已知甲工程队每月施工费用为15万元，比乙工程队多6万元，按要求该工程总费用不超过141方元，工程必须在一年内竣工（包括12个月）．为了确保经费和工期，采取甲、乙工程队同时开工，甲工程队做a个月，乙工程队做b个月（a、b均为整数）分工合作的方式施工，问有哪几种施工方案？

【分析】（1）设乙队需要x个月完成，根据题意列方程即可得到结论；（2）根据费用不超过141万元列出一元一次不等式求解即可．

∴b为3的倍数，∴b＝9或b＝12．

当b＝9时，a＝4；当b＝12时，a＝2∴a＝4，b＝9或a＝2，b＝12．

方案一：甲队作4个月，乙队作9个月；方案二：甲队作2个月，乙队作12个月；

【点评】本题考查了分式方程的应用及一元一次不等式的应用，解题时，可把总工程量看做"1"．此题主要考查列分式方程（组）解应用题中的工程问题．分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．用不等式组解决实际问题时，要注意问题的答案既要符合不等式组的要求，又要符合实际问题的意义和限制．如本题中比赛的场数应为非负整数．

方法归纳：以上涉及参数问题都需在熟悉不等式的性质基础上，熟练掌握不等式及不等式组解法的前提下解决;同时，应灵活使用"数轴"及"口诀"寻找解题策略，并学会归纳总结，及时巩固方法思路.我们在教学中，要注意培养学生的逆向思维，开阔思路，养成周密灵活、全面思考问题的良好习惯，这对提高我们分析问题、解决问题的能力，无疑是有好处的.

专题新题精炼