数列时每年高考的必考项目，下面介绍如何运用数学思想方法巧做数列题；

1．函数与方程思想

处理数列与方程、函数知识相交汇的问题，经常运用函数与方程的思想。数列可以视为一种定义域为正整数的有限子集的函数，当自变量从小到大取值时，其相对应的一系列函数值，因此在研究某些数列问题时，利用函数思想即可容易理解数列问题的本质，又可以简化运算。

2．分类讨论数学思想

遇到数列中的交汇知识问题时，有时候需要利用分类讨论思想来解决较为简单。比如等比数列的公比为字母的求和问题，经常需要对公比是否为1进行分类讨论；由Sn求an时，常常需要对n的数值进行分类讨论等等；通过分类讨论，可以将复杂的数列问题简单化，但解题时，需要注意确定分类的标准。

3．化归与转化思想

有关数列与其他知识（不等式/新定义等）相结合的问题，常常需要利用划归与转化思想，思想的核心是把生题转化为熟题，解题的过程就是一个缩小已知与求解的差异的过程，通过划归，转化为两类特殊的等差或等比数列问题，就可以顺利地进行解析。

从几个常考的命题角度，并举例分析应用数学思想的解题思路。

命题角度1 数列与逻辑命题结合

命题角度2 数列与新定义结合

思路分析：

（1）利用等比数列的通项公式与递推公式证明；

（2）利用数列新定义和等差数列的定义证明。

解题策略： 解答此类新定义数列题的关键点为：一是认真审题，读明白新定义数列的含义；二是活用新定义，即会利用等差/等比数列的定义，判断数列为等差/等比数列，则可利用等差/等比数列的前n项和的公式求和，并活用等差/等比数列的性质。

命题角度3 数列与方程结合

命题角度4 数列与函数结合

解题策略： 本题的关键是要根据函数的导数、（切线）直线方程求得数列的基本量，计算出数列的通项公式；数列求和要根据数列的通项公式选择合适的求和方法，本题中数列的通项公式是一个等差数列与一个等比数列的相应两项乘积，可以利用错位相减法进行求和；若数列的通项公式的分母是一个等差数列相邻2项的乘积，则可以利用裂项相消法进行求和。

命题角度5 数列与不等式结合

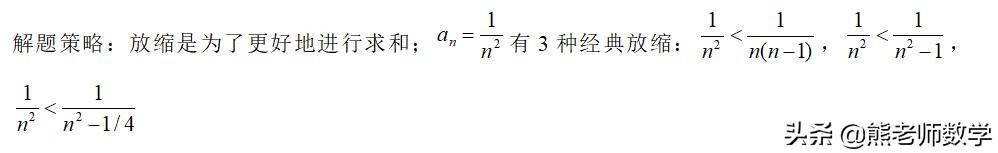
解题策略：放缩是为了更好地进行不等式的转化，利用划归的数学思想，将不熟悉的代数式转化为熟悉的等比通项，即可顺利地进行证明求解；