小升初：拉丁方问题

如图1的每个方格中分别填入1、2、3、4、5、6、7中的一个数，使得每行、每列的七个数各不相等；并且圆圈中的数等于与它相邻的四个数的乘积．那么，★处所填的数是 ．

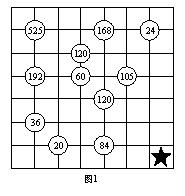
[解析]这是一道拉丁方问题．每行、每列的7个各不相等的数的乘积均为7!=5040．任意两行、两列中14个各不相等的数的乘积均为7!*7!=25401600，除去已知的乘积，未知数的乘积便可知．将其分解，进行分析，即可填出．首先将列依次定a、b、c、d、e、f、g，行依次定为1、2、3、4、5、6、7，那么★处可表示为7g．观察a、b两列，由25401600/525/192/36=7，容易知道7a、7b只能是1和7．再由6b、6c、7b、7c相乘积为20，容易知道7b只能填1，7a只能填7．

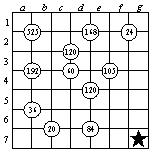
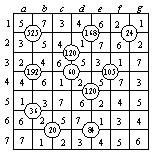
由于6b、6c、7b、7c相乘积为20，7b填1，这样一来，6b、6c、7c可能填1、4、5或2、2、5．若6b、6c、7c填1、4、5，只能是6b填4，6c填1，7c填5（1a，1b，2a，2b乘积为525，1a，1b，2a，2b中必有两个是5，一个是3，另一个是7）．于是5a、5b、6a的乘积为9，在5a、5b、6a中，必有两个是3，这时与1a，1b，2a，2b中所填的3出现在同一列，矛盾．确定1c、2c中填的数．由25401600/525/168/24=12，12=2*6=3*4，7c已填2，所以1c、2c只能填3和4．60与120均不是7的倍数，故c列中，7只能在5c处．3c、4c只能填1和6．60与120均是5的倍数，故c列中，5已出现，显然3d填5，4d填2．再由24501600/168/120/84=15，15=3*5，可确定3e填3．下面确定4e，4e所填的数是105与120的公约数，只能是1或5．若填1，则5d、5e的乘积为60，它显然不能表示成两个不大于7的数的乘积，故4e填5．从第6、7行看，6d、6e、7d、7e不能出现2，这样一来，84只能表示为84=7*3*4*1，显然6d、6e只能填7和1，7d填3，7e填4，．5d、5e乘积是120/2/5=12，从d、e列看，12只能表示为12=2*6，5d填6，5e填6．下面请同学们自己进行分析，容易得到下面填法．★处所填的数是6．