二级结论真的好

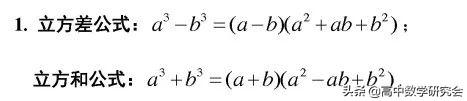
5. 平行四边形对角线平方之和等于四条边平方之和.

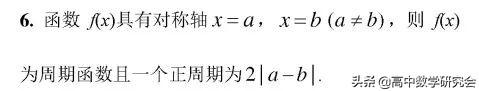
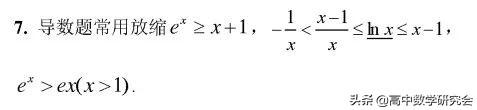
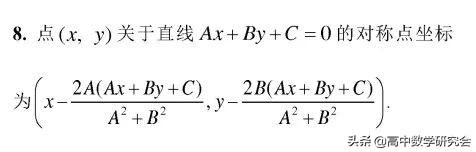
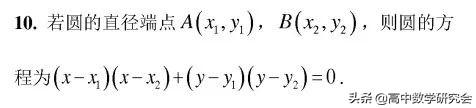
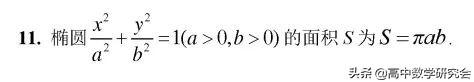
12. 过椭圆准线上一点作椭圆的两条切线，两切点连线所在直线必经过椭圆相应的焦点.

13. 圆锥曲线的切线方程求法：隐函数求导.

推论：

14. 切点弦方程：平面内一点引曲线的两条切线，两切点所在直线的方程叫做曲线的切点弦方程.

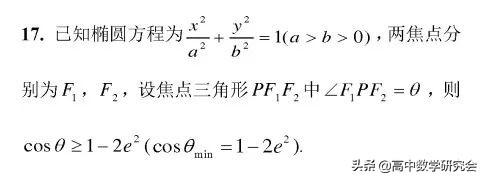
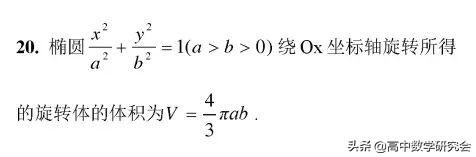
22. 过椭圆上一点做斜率互为相反数的两条直线交椭圆于A、B两点，则直线AB的斜率为定值.

24. 抛物线焦点弦的中点，在准线上的射影与焦点F的连线垂直于该焦点弦.

25. 双曲线焦点三角形的内切圆圆心的横坐标为定值a(长半轴长).

26. 对任意圆锥曲线，过其上任意一点作两直线，若两直线斜率之积为定值，两直线交曲线于A，B两点，则直线AB恒过定点.

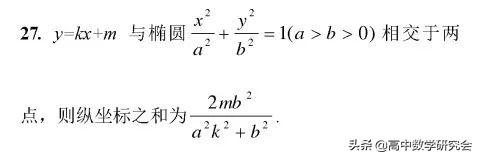
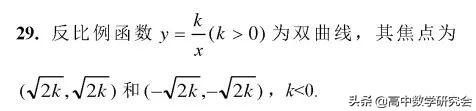
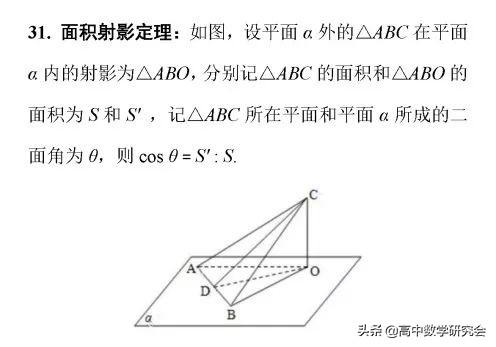
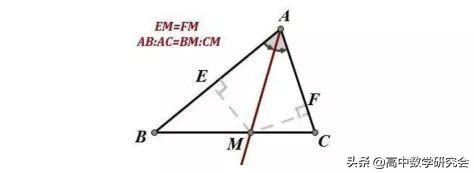
32. 角平分线定理：三角形一个角的平分线分其对边所成的两条线段与这个角的两边对应成比例。

角平分线定理逆定理：如果三角形一边上的某个点分这条边所成的两条线段与这条边对角的两边对应成比例，那么该点与对角顶点的连线是三角形的一条角平分线.

39. 帕斯卡定理：如果一个六边形内接于一条二次曲线(椭圆、双曲线、抛物线)，那么它的三对对边的交点在同一条直线上.

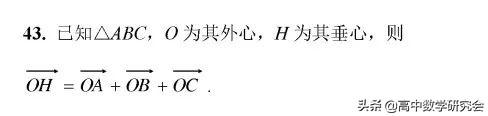
45. 三角形五心的一些性质：

(1)三角形的重心与三顶点的连线所构成的三个三角形面积相等；

(2)三角形的垂心与三顶点这四点中，任一点是其余三点所构成的三角形的垂心；

(3)三角形的垂心是它垂足三角形的内心；或者说，三角形的内心是它旁心三角形的垂心；

(4)三角形的外心是它的中点三角形的垂心；

(5)三角形的重心也是它的中点三角形的重心；

(6)三角形的中点三角形的外心也是其垂足三角形的外心；

(7)三角形的任一顶点到垂心的距离，等于外心到对边的距离的二倍.