初中数学：证比例式或等积式的技巧

证比例式或等积式，若遇问题中无平行线或相似三角形时，则需要构造平行线或相似三角形，得到等比例线段；若比例式或等积式中的线段分布到两个三角形或不在两个三角形中，可尝试证这两个三角形相似或先将它们转化到两个三角形中再证其相似；若在两个明显不相似的三角形中，可运用中间比代换。具体详见以下例题。

技巧一：构造平行线法

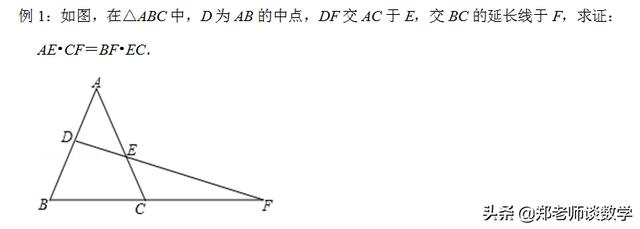
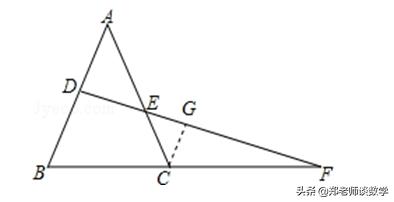
【点评】本题主要考查了相似三角形的判定及其性质的应用问题，解题的关键是通过作辅助线构造相似三角形．

技巧二：构造相似三角形法

【分析】先作辅助线DG∥BC，然后根据三角形相似的知识可以得到结论成立，从而可以解答本题．

【解答】证明：作DG∥BC，

则△ADG∽△ABC，△DGF∽△ECF，

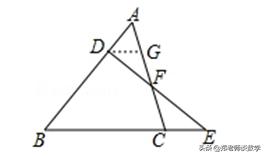
【点评】本题考查相似三角形的判定与性质，解答本题的关键是明确题意，找出所求结论需要的条件，利用三角形的相似解答．

技巧三：三点定型法

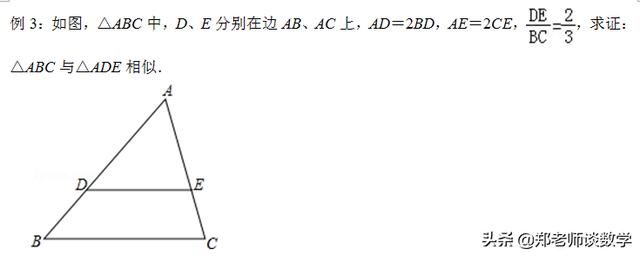
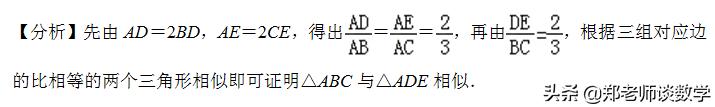
【点评】本题考查了相似三角形的判定，判定两个三角形相似有四种方法：

（1）平行线法：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似；

（2）三边法：三组对应边的比相等的两个三角形相似；

（3）两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似；

（4）两角法：有两组角对应相等的两个三角形相似．

技巧四：等积过渡法

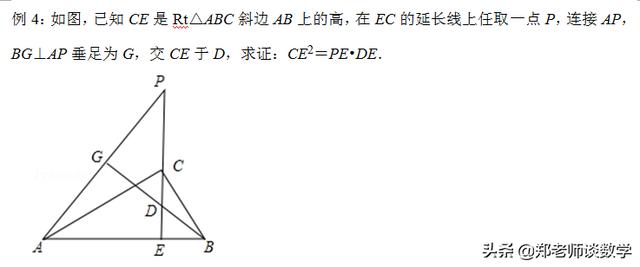
【分析】首先证Rt△ACE∽Rt△CBE，得出CE2＝AE•BE（即射影定理）；再通过证△AEP∽△BED，得出PE•DE＝AE•BE，联立上述两式即可得出本题要证的结论．

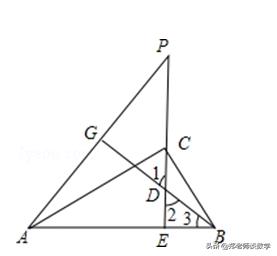
【点评】此题主要考查的是相似三角形的判定和性质．