巧用位似解三角形中的内接多边形问题

先跟大家普及一些知识：位似图形是特殊位置的相似图形，它具有相似图形的所有性质；位似图形必须具备三个条件：（1）两个图形相似；（2）对应点的连线相交于一点；（3）对应边互相平行或在同一直线上。今天我们将跟大家讲讲如何巧用位似解三角形中的内接多边形问题。

类型一：三角形的内接正三角形问题

例1：如图，用下面的方法可以画△AOB的内接等边三角形，阅读后证明相应问题．

画法：

①在△AOB内画等边△CDE使点C在OA上，点D在OB上；

②连结OE并延长，交AB于点E′，过点E′作E′C′∥EC，交OA于点C′，作E′D′∥ED，交OB于点D′；

③连结C′D′，则△C′D′E′是△AOB的内接三角形．求证：△C′D′E′是等边三角形．

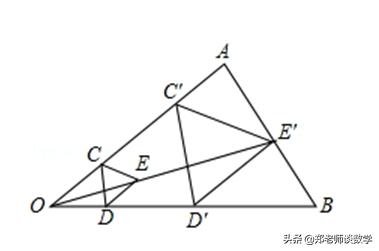
【分析】根据作法可知：E′C′∥EC，E′D′∥ED，可证得△OCE∽△OC′E′，△ODE∽△OD′E′，根据相似可证得对应边的比相等，对应角相等，即可根据对应边的比成比例且夹角相等的三角形相似，可证得△CDE∽△C′D′E′，即可得结果．

【解答】证明：∵E′C′∥EC，E′D′∥ED，

∴△OCE∽△OC′E′，△ODE∽△OD′E′，

∴CE：C′E′＝OE：OE′，DE：D′E′＝OE：OE′，∠CEO＝∠C′E′O，∠DEO＝∠D′E′O，

∴CE：C′E′＝DE：D′E′，∠CED＝∠C′E′D′，

∴△CDE∽△C′D′E′，

∵△CDE是等边三角形，

∴△C′D′E′是等边三角形．

【点评】此题主要考查了相似三角形的判定与性质以及位似图形的性质，利用相似图形的性质得出是解题关键．

类型二：三角形的内接矩形问题

例2：如图，求作内接于已知三角形ABC的矩形DEFG，使它的边EF在BC上，顶点D，G分别在AB，AC上，且DE：EF＝1：2．

【分析】先确定位似中心，再分别连接并延长位似中心和能代表原图的关键点；接着根据位似比，确定能代表所作的位似图形的关键点；然后顺次连接上述各点，得到放大或缩小的图形．

【解答】解：如图，先任意作MN∥BC，再作矩形MNPQ，使MQ：MN＝1：2，分别连接AQ、AP，它们的延长线交BC于E、F，再分别作DE⊥BC交AD于D，GF⊥BC交AC于G，则可得矩形DEFG．

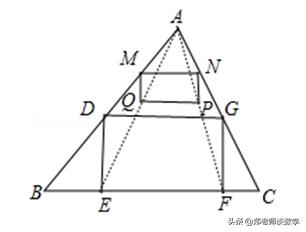
故矩形DEFG即为所作．

【点评】本题考查了作图﹣位似变化以及矩形的判定与性质的运用，解决问题时注意：画一个图形的位似图形时，位似中心的选择是任意的，这个点可以在图形的内部或外部或在图形上，而对于具体问题要考虑画图方便且符合要求．

类型三：三角形的内接正方形问题

例3：如图，在Rt△ABC中，AB＝BC，∠B＝90°，AC＝10．四边形BDEF是△ABC的内接正方形（点D、E、F在三角形的边上）．则此正方形的面积是多少？

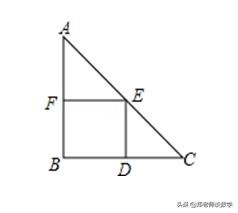
【分析】由已知可得到△AFE∽△ABC，根据相似三角形的边对应成比例即可求得EF的长，进而根据正方形的面积公式即可求得．

【点评】主要考查了正方形基本性质和比例线段的运用．解题的关键是准确的找到相似三角形并根据其相似比列方程求解．

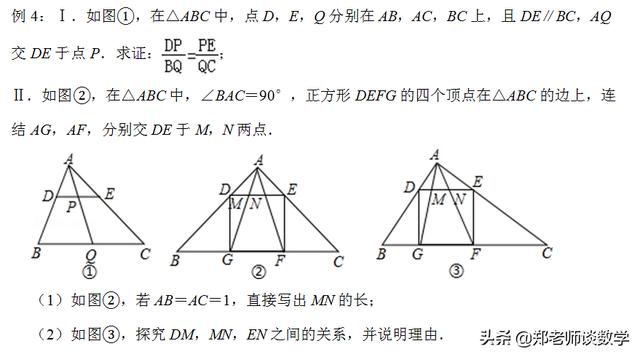
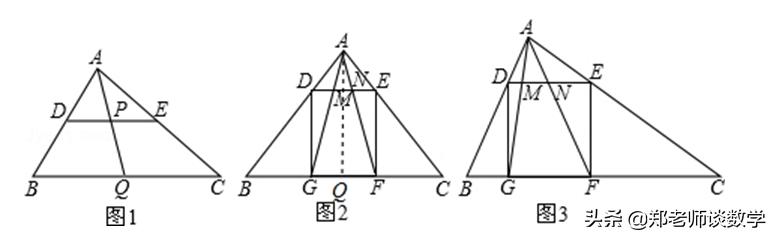
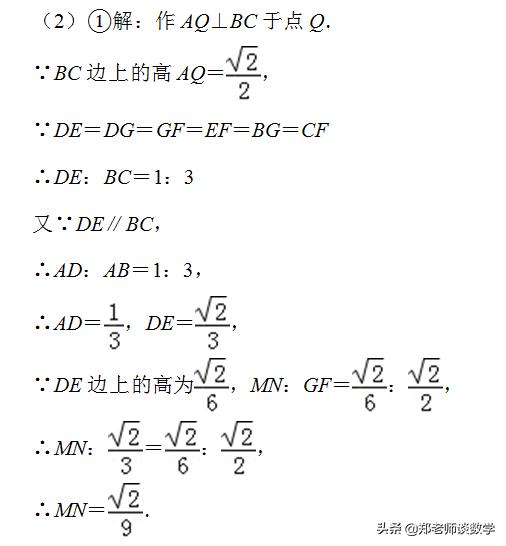
【点评】本题考查了相似三角形的判定和性质以及正方形的性质，是一道综合题目，注意利用相似三角形的对应边成比例解决问题．