追及问题

追及问题是行程问题中相当经典的一类题型，一般题目中会出现两个物体同方向运动，并且速度之间有不同(快、慢)，后者追上前者的问题。那么在解决这类问题的时候一定要抓住一个关键点“速度差”，然后借助线段图来分析问题就可以正确求出结果。

基础例题

1、甲骑自行车从A地到B地，每小时行16千米，1小时后，乙也骑自行车从A地到B地，每小时行20千米，结果两人同时到达B地。A、B两地相距多少千米？

这是一道非常基础的直线追及问题，我们先来看，甲先出发1小时后，乙才出发，并且甲的速度是16千米每小时，那么说明了甲、乙的追及路程就是16千米，如下图：

我们继续来看，再过1个小时后，甲、乙两人之间的距离为多少，那么甲再过1小时就应该行至32千米处，乙过1小时就应该行至20千米处，如下图：

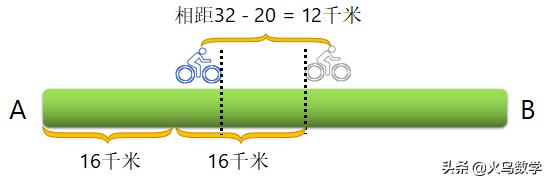
我们可以看到过1个小时后，两者之间的追及距离减少了4千米，因为乙每小时比甲多走20 - 16 = 4千米。所以相差16千米，需要追上的时间就为16 ÷ 4 = 4时。并且题目又告诉那我们我们，两人同时达到B地，也就是当甲追上乙恰好走完全程，所以全程就为20 × 4 = 80千米。

精讲例题

2、甲、乙两人以每分钟60米的速度同时、同地、同向步行出发。走15分钟后甲返回原地取东西，而乙继续前进。甲取东西用去5分钟的时间，然后改骑自行车以每分钟360米的速度追乙，甲骑车多少分钟才能追上乙？

这道题中所提供的数量关系非常多，所以一定要仔细分析，我们来一步一步画图：

走了15分钟后， 15分钟就走了15 × 60 = 900米，甲返回原地取东西，乙继续前期，这如下图：

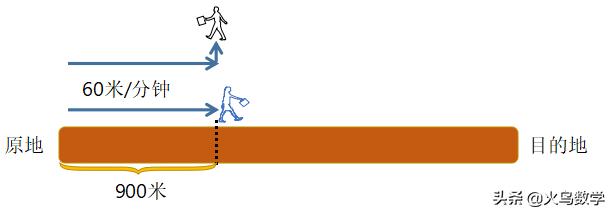
那么甲原路返回速度不变，那么所以的时间也是15分钟，所以当甲回到原地的时候，乙在这15分钟又走了900米，如下图：

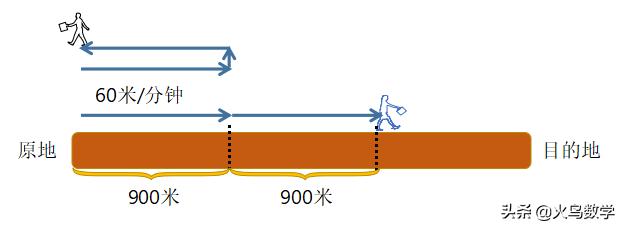
当甲到达原地的时候，又花了5分钟时间取东西，而此时乙继续向前走5分钟，应该走了5 × 60 = 300 米。如下图：

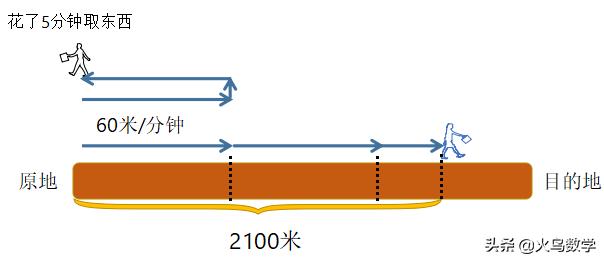
那么我们可以看到此时甲、乙之间相距了2100米，也就是追及路程。接下来甲换骑自行车以每小时360米的速度去追乙，如下图：

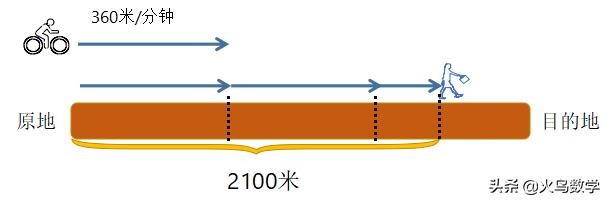
我们知道换骑自行车之后甲每分钟比乙多走360 - 60 = 300米，追及路程为2100米，所以追及所花的时间为2100 ÷ 300 = 7分钟，就可以追上乙。这道题很容易被忽略的一点就是甲取东西所花去的5分钟时间，乙继续前进，所以一定要仔细分析读题。

思考题

汽车以每小时30千米的速度从甲地出发，6小时后能到达乙地。汽车出发1小时后原路返回甲地取东西，然后立即从甲地出发，为了能在原定时间内到达乙地，汽车必须以每小时多少千米的速度从甲地驶向乙地？