《导数》解答题：三种常见方法解决不等式恒成立求参数范围

这是一道与三角函数相关的导数题，先看题吧

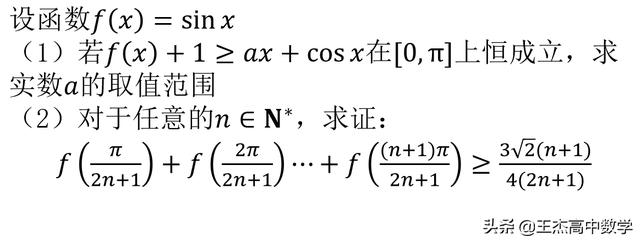
第一问是比较常见的已知不等式恒成立，求参数的取值范围问题，此种题型常见的解法有三种

方法一：移项，含参求导，分类讨论，这种方法的难点在于如何搞清楚分类讨论的标准【结合三角函数的图像】

方法二：分离参数，转化为函数最值问题，可能需要用到洛必达法则

方法三：利用代入几个特殊值【取交集】，先猜再证

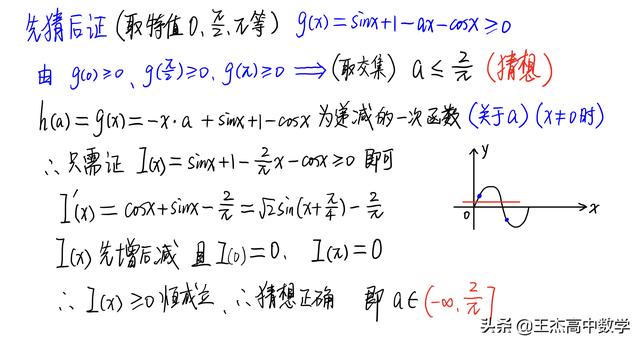
第二问是不等式的证明问题，看似与第一问没关系，但实质上必然要利用第一问的结论【如果用不到的话，出题者也不会把这看似没关系的两个小问放在同一个题目中】，是“暗示”，更是“明示”

利用第一问中的端点值，然后放缩，还需结合到等差数列的前n项和