平行线的判定和性质中几种常用的作辅助线的方法

在解决平行线的问题时，当无法直接得到角的关系或两条线之间的位置关系时，通常借助辅助线来帮助解答。如何作辅助线需根据已知条件确定，辅助线的添加既可以产生新的条件，又能将题目中原有的条件联系起来，所以说一条好的辅助线是几何的生命线，作好辅助线可以起到事半功倍的效果。今天我们将介绍三种类型的作辅助线的方法，希望对大家的学习有帮助。

类型一：加截线（连接两点或延长线段相交）

例1：如图，AB∥EF，CD⊥EF，∠BAC=50°，则∠ACD＝（ ）

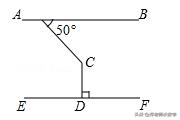
A．120° B．130° C．140° D．150°

【分析】如图，作辅助线；首先运用平行线的性质求出∠DGC的度数，借助三角形外角的性质求出∠ACD即可解决问题．

【解答】解：如图，延长AC交EF于点G；

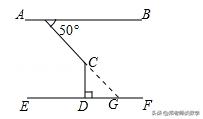
∵AB∥EF，

∴∠DGC＝∠BAC＝50°；

∵CD⊥EF，

∴∠CDG＝90°，

∴∠ACD＝90°+50°＝140°，

故选：C．

【点评】该题主要考查了垂线的定义、平行线的性质、三角形的外角性质等几何知识点及其应用问题；解题的方法是作辅助线，将分散的条件集中；解题的关键是灵活运用平行线的性质、三角形的外角性质等几何知识点来分析、判断、解答．

类型二：过“拐点”作平行线

例2：（1）如图1，AB∥CD，E为AB、CD之间的一点，已知∠B＝40°，∠C＝30°，求∠BEC的度数．

（2）如图2，AB∥ED，试探究∠B、∠BCD、∠D之间的数量关系．

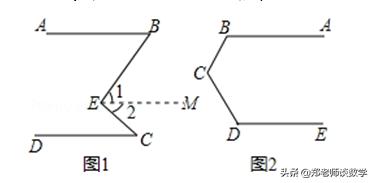
【分析】（1）利用平行线的判定与性质完成即可；

（2）与（1）题类似，过点C作CF∥AB利用平行线的性质即可得到结论．

【解答】解：（1）过点E作EM∥AB，

∴∠B＝∠1（两直线平行，内错角相等）．

∵AB∥CD，AB∥EM，

∴EM∥CD（平行于同一直线的两条直线平行）．

∴∠2＝∠C（两直线平行，内错角相等）．

∴∠BEC＝∠1+∠2＝∠B+∠C＝40°+30°＝70°．

（2）如图，过点C作CF∥AB

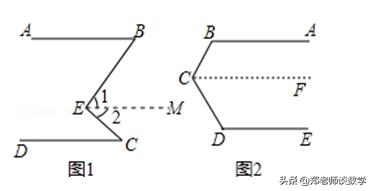
∴∠B+∠BCF＝180°（两直线平行，同旁内角互补）．

∵AB∥DE，AB∥CF，

∴CF∥ED（平行于同一直线的两条直线平行）．

∴∠D+∠DCF＝180°（两直线平行，同旁内角互补）．

∴∠B+∠BCD+∠D＝360°．

【点评】本题考查了平行线的性质与判定，正确的作出辅助线是解答本题的关键．

类型三：平行线间多折点角度问题探究

例3：探究：

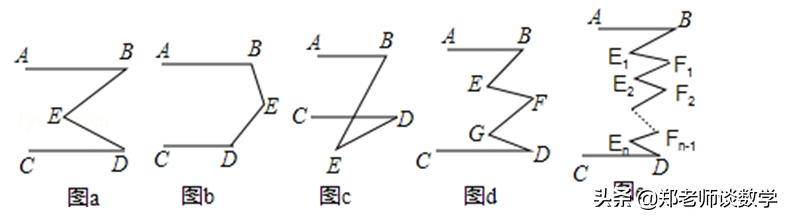
（1）如图a，若AB∥CD，则∠B+∠D＝∠E，你能说明为什么吗？

（2）反之，若∠B+∠D＝∠E，直线AB与CD有什么位置关系？请证明；

（3）若将点E移至图b所示位置，此时∠B、∠D、∠E之间有什么关系？请证明；

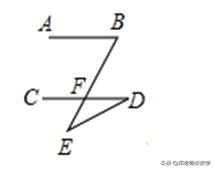
（4）若将E点移至图c所示位置，情况又如何？

（5）在图d中，AB∥CD，∠E+∠G与∠B+∠F+∠D又有何关系？

（6）在图e中，若AB∥CD，又得到什么结论？

【分析】已知AB∥CD，连接AB、CD的折线内折或外折，或改变E点位置、或增加折线的条数，通过适当地改变其中的一个条件，就能得出新的结论，给我们创造性的思考留下了极大的空间，解题的关键是过E点作AB（或CD）的平行线，把复杂的图形化归为基本图形．

【解答】解：（1）过E作EF∥AB，

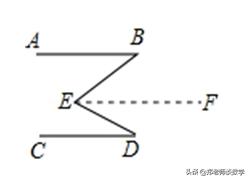
则∠B＝∠BEF，

∵AB∥CD，

∴EF∥CD，

∴∠D＝∠DEF，

∴∠BED＝∠BEF+∠DEF＝∠B+∠D．

（2）若∠B+∠D＝∠E，由EF∥AB，∴∠B＝∠BEF，

∵∠E＝∠BEF+∠DEF＝∠B+∠D，

∴∠D＝∠DEF，∴EF∥CD，

∴AB∥CD；

（3）若将点E移至图b所示位置，过E作EF∥AB，

∴∠BEF+∠B＝180°，∵EF∥CD，∴∠D+∠DEF＝180°，

∠E+∠B+∠D＝360°；

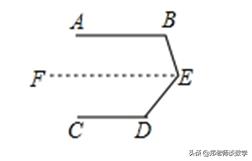
（4）∵AB∥CD，∴∠B＝∠BFD，

∵∠D+∠E＝∠BFD，

∴∠D+∠E＝∠B；

（5）∵AB∥CD，∴∠E+∠G＝∠B+∠F+∠D；

（6）由以上可知：∠E1+∠E2+…+∠En＝∠B+∠F1+∠F2+…+∠Fn﹣1+∠D；

【点评】本题考查了平行线的性质与判定，属于基础题，关键是过E点作AB（或CD）的平行线，把复杂的图形化归为基本图形．