中考热点：三法破解坐标系下的几何图形规律探究问题

新的课程课标中明确要求：用代数式表示数量关系及所反映的规律，发展学生的抽象思维能力。根据一列数或一组图形的特例进行归纳，猜想，找出一般规律，进而列出通用的代数式，称之为规律探究。在历年的中考或学业水平考试中屡见不鲜，频繁考查，考生大都感到困难重重，无从下手，导致丢分。

解决此类问题的关键是："细心观察，大胆猜想，精心验证"。 笔者认为：只要善于观察，细心研究，知难而进，就会走出"山穷水尽疑无路"的困惑，收获"柳暗花明又一村"的喜悦。坐标系背景下几何图形规律探究问题更是令很多学生困惑，这一类题目一般是结合常见的几何图形，如等腰三角形、等边三角形、正方形、点在平面直角坐标系中的变化、函数图像等进行考察，一定要把握几何图形的特殊性质，然后从特殊到一般找规律即可。

例题：平面直角坐标系xOy中，点A₁，A₂，A₃，…和B₁，B₂，B₃，…分别在直线y＝1/5x+b和x轴上．△OA₁B₁，△B₁A₂B₂，△B₂A₃B₃，…都是等腰直角三角形，如果A₁（1，1），

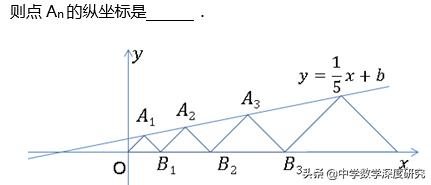
本题似曾相识燕归来，好像做过，穿了个马甲就不认识了？别急，这个图确实以前做过，不过，这次的条件不一样了，难度稍微增加了一点点。我们先分析完这道题，看一下能有几种方法来求解。

先看已知条件：A₁坐标已知，直线的解析式包含一个未知参数，将点A坐标代入，易得4/5，所以直线解析式为y=1/5x+4/5,由图，ΔOA₁B₁为等腰直角三角形，可得B₁点坐标（2，0）。

接下来的目标自然是求A₂的坐标。这一步也是本题解决的关键。方法有很多，这里介绍三个典型解法：

方法一，几何法：

设A₂（x，y），如图，有B₁N=A₂N，所以x=2+y，代入直线解析式，可得A2点坐标(7/2,3/2), 类似地，得到A₃点坐标(29/4, 9/4)，

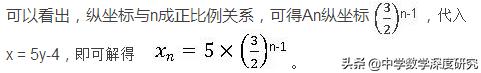
方法二，代数法：

直线B₁A₂过点B₁且斜率为1，可得B₁A₂的解析式为y=x-2，与直线A₁A₂解析式连立，可求得点A₂的坐标，类似地，求得点A₃的坐标。

方法三，比例法：

根据等比缩放原理，图中等腰直角三角形的边长以此等比例放大，只需要找出B₁A₂与OA₁的比值，就可以求出An的纵坐标了。观察ΔPOA₁与ΔPB₁A₂，有B₁A₂：OA₁=PB₁：PO。故此，求出P点坐标（-4，0）后，可秒得结果。

好了，三种解法介绍完了。一般地，对于直角坐标系规律题，代数法与比例法较为通用，但代数法一般计算较多，稍显繁琐，比例法往往比较快捷，但对我们的水平要求稍高一点。

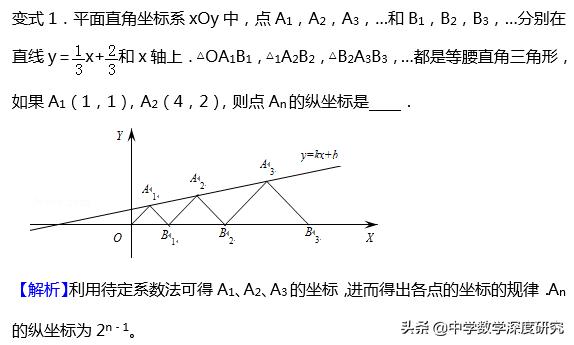
牛刀小试：

1．（2018•罗平县三模）在平面直角坐标系xOy中，正方形A₁B₁C₁O、A₂B₂C₂B₁、A₃B₃C₃B₂，…，按图所示的方式放置．点A₁、A₂、A₃，…和点B₁、B₂、B₃，…分别在直线y＝kx+b和x轴上．已知C₁（1，﹣1），C₂（7/2，-3/2），则点A₃的坐标是______ ．

2（2018•贵港中考题）如图，直线l为y＝√3x，过点A₁（1，0）作A₁B₁⊥x轴，与直线l交于点B₁，以原点O为圆心，OB₁长为半径画圆弧交x轴于点A₂；再作A₂B₂⊥x轴，交直线l于点B₂，以原点O为圆心，OB₂长为半径画

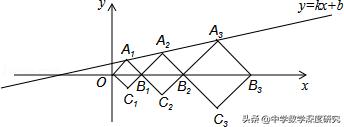
3．（2018•淮安中考题）如图，在平面直角坐标系中，直线l为正比例函数y＝x的图象，点A₁的坐标为（1，0），过点A₁作x轴的垂线交直线l于点D₁，以A₁D₁为边作正方形A₁B₁C₁D₁；过点C₁作直线l的垂线，垂足为A₂，交x轴于点B₂，以A₂B₂为边作正方形A₂B₂C₂D₂；过点C₂作x轴的垂线，垂足为A₃，交直线l于点D₂，以A₃D₃为边作正方形A₃B₃C₃D₃，…，按此规律操

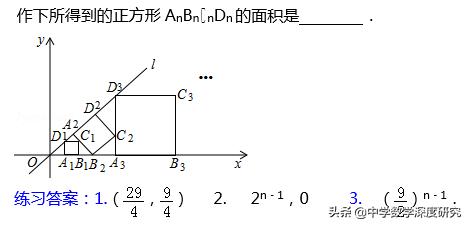
一般地，对于一次函数找规律题目，要先找出前面几个点的坐标，找到其规律性，然后推导出第N个点坐标的一般表达式，找到第n个图形与第n+1个图形之间的大小比例关系是解决此类题目的关键。