二次函数图象信息问题解法口诀

已知二次函数y=ax^2+bx+c的图象，确定系数a、b、c及由a、b、c组合而成的代数式的符号是中考中常见的问题。如何解答这类问题呢？请看如下口诀：

a的符号看开口；b要结合对称轴，

左同右异不难记；y轴交点确定c；

遇到根的判别式，横轴交点个数定；

系数组合看象限，取值尝试自变量。

口诀翻译：

"a的符号看开口"的意思是：确定a的符号看抛物线的开口方向。如果开口向上，则a>0；如果开口向下，则a<0；

"b要结合对称轴，左同右异不难记"的意思是：要确定b的符号，先看对称轴x=-b/2a是在y轴的左侧还是右侧？如果在y轴的左侧，则x=-b/2a<0，b/a>0，从而b与a同号，简称"左同"； 如果在y轴的右侧，则x=-b/2a>0，b/a<0，从而b与a异号，简称"右异"；

"y轴交点确定c"的意思是：抛物线与y轴的交点位置确定c的符号。如果交点在y正半轴，则c>0；如果交点在y负半轴，则c<0；如果交点在原点，则c=0；

"遇到根的判别式，横轴交点个数定"的意思是：根的判别式b^2-4ac的符号由抛物线与x轴的交点个数确定。如果有两个交点，则b^2-4ac>0；如果只有一个交点，则b^2-4ac=0；如果没有交点，则b^2-4ac<0；

"系数组合看象限，取值尝试自变量"的意思是：判断由系数a、b、c组合而成的代数式f(a、b、c)的符号，对自变量x取某个值n，使得函数值y= f(a、b、c)，然后看点[n，f(a、b、c)]所在的象限。如果点[n，f(a、b、c)]在第一、二象限，则f(a、b、c)>0；如果点[n，f(a、b、c)]在第三、四象限，则f(a、b、c)<0；如果点[n，f(a、b、c)]在x轴上，则f(a、b、c)=0。

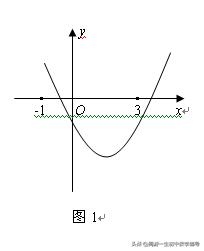
例1已知二次函数y=ax^2+bx+c的图象如图1所示，给出如下结论：

①abc>0；②b^2>4ac；③a-b+c>0；

④a+b+c<0；⑤4a-2b+c<0.

其中正确的有（ ）

A．2个 B。3个 C。4个 D。5个

解析：由抛物线开口向上，知a>0；由对称轴在y轴的右侧，知b与a的符号相异，所以b<0；由与y轴的交点在负半轴，知c<0.所以abc>0，①正确；

由抛物线与x轴有两个交点，知b^2-4ac>0，所以b^2>4ac，②正确；

当x=-1时，y=a-b+c，由点（-1，a-b+c）在第二象限，知a-b+c>0，所以③正确；

当x=1时，y=a+b+c，由点（1，a+b+c）在第四象限，知a+b+c<0，所以④正确；

当x=-2时，y=4a-2b+c，由点（-2，4a-2b+c）在第二象限，知4a-2b+c>0，所以⑤错误。

综上，选C。

例2 已知抛物线y=ax^2+bx+c如图2所示，确定a、b、c及3a+c的符号。

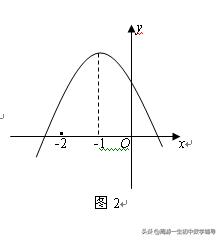
解析：由图象可知：开口向下，与y轴交点在正半轴，对称轴为x=-1，与x轴有两个交点，且其中一个交点在（-2，0）左边。

因此，a<0，b<0，c>0；

由对称轴x=-1，得-b/2a=-1，b=2a.

所以3a+c=a+2a+c=a+b+c，

因为点（-2，0）关于抛物线对称轴x=-1的对称点为（1，0），点（-2，0）在抛物线与x轴两个交点之间，所以点（1，0）也在抛物线与x轴两个交点之间，所以点（1，a+b+c）在第一象限，所以a+b+c>0，

所以3a+c>0.