中考专题复习——几何题利用旋转构造“手拉手”模型

在初中数学当中，旋转是解决几何问题的常用的技巧之一，今天给大家分享一个通过旋转，构造手拉手模型的方法。

如图，△ABD，△BCE为等边三角形

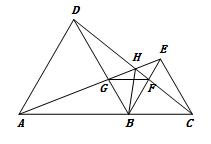
从已知条件可得出以下结论：

（1）△ABE≌△DBC

（2）△ABG≌△DBF

（3）△CFB≌△EGB

（4）△BFG为等边三角形

（5）△AGB∽△DGH

（6）∠DHA＝60°

（7）H，G，F，B四点共圆

（8）BH平分∠AHC ……

那么在△ABE与△DBC中，这两个全等的三角形除了对应边相等，对应角相等外，还有什么共同特征呢？

通过观察不难发现，我们也可以把△DBC看作由△ABE绕点B逆时针旋转60°得到．

通过该例题，我们可以看到，这两个三角形他们具有公共顶点B,且具有相等的线段。所以以后遇到等线段，共顶点的两个全等三角形，我们一般可以考虑旋转．

因此“手拉手模型”可以归纳为：等线段，共顶点，一般用旋转．

接下来，我们通过一个小例题，来应用下刚才所学到的知识。

1．如图1，△BAD中，∠BAD＝45°，AB＝AD，AE⊥BD于E，BC⊥AD于C， 则AF＝____BE．

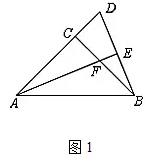
分析：不难看出，题1中，等线段是AC，BC，共顶点是C，△ACF绕点C逆时针旋转90°得△BCD．所以可知AF=BD，因此可以得出AF=2BE.

2．如图2，△ABC和△BED均为等边三角形，ADE三点共线，若BE＝2，CE＝4，则AE＝______．

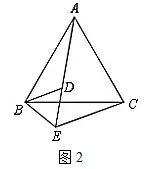
分析：题2中，等线段是AB，BC，共顶点是B，△ABD绕点D顺时针旋转60°得△CBE．因此，可知AD=CE=4,BE=DE=2,所以AE=6

例3：等边△ABC中，AD＝4，DC＝3，BD＝5，求∠ADC度数．

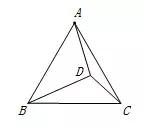
分析：因为是等边三角形，所以该题中隐藏着手拉手模型。不难发现，AB＝AC，A为“公共顶点”，所以，我们可以通过旋转去构造出全等三角形。

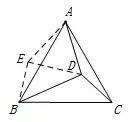
故将AD绕点A顺时针旋转60°到AE，连接BE，DE．则△ADE也为等边三角形．易证△AEB≌△ADC，∴BE＝DC＝4，根据勾股定理逆定理，可证∠BED＝90°，则∠AEB＝∠ADC＝150°

.自主练习

1．如图，在四边形ABCD中，AD＝4，CD＝3，∠ABC＝∠ACB＝∠ADC＝45°，则BD的长为 _________．

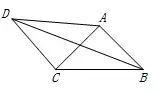
分析：由题意可知，AC=AB,公共顶点是A点，所以该题可以利用旋转构造全等三角形，