有时候初中几何题难做，大多是因为辅助线不好找，没有思路，于是过多去思考辅助线的技巧，当旁人稍稍点明以后总有恍然大悟的感觉，其实通过认真观察研究会发现，证明题作完辅助线以后所得图形离基本离不今天要说的：

• 平面几何三大基本变换，平移、旋转和对称

观察问题将所要求证的与“基础知识”联系起来才是我们解决问题的根本方法，平时先理清知识再去练习技巧和总结方法， 解题的时候可以先找是否可以利用这三大变换，解完题以后再去回顾相关知识，慢慢就能达到常说的做一题通一类。

• 平常说的一题多解往往就是因为经过各种变换之后可以利用不同的知识进行求解，一题多解只是方法，总结这些方法用的相关知识才是能力的提升，比如哪些是对称，哪些是旋转。

• 初中几何证明题中基本的许多性质都源于图形本身的"变换特征"，初中阶段最为重要和最为常用的图形关系"全等三角形"在很多情况具有"变换"形式的联系.两个三角形全等本是指它们的形状和大小都一样，和相互间的位置没有直接关系，但是，在同一个问题中涉及三角形关系的时候，大多数都和位置相关，成轴对称关系（有时候表现为折叠），或成平移的关系，或成旋转的关系（包括中心对称）。因此，在解决具体的几何相关问题时，如果我们有意识地从所求出发，结合图形的关系中所显示或暗示的"变换特征"，从而识别、构造出基本图形或图形关系，这将对解决问题有着极为重要的启发和引导的作用.接下来我们从变换视角以题目中三角形的全等关系为主进行研究.

下面以两个"旋转"类题目进行分析。

• 解决几何类型问题的能力，关键是要善于从综合与复杂的图形中识别然后构造出基本图形及基本的图形关系，而"变换"的概念和思路能很好地提高我们这种识别和构造的能力.

例1、 已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．

（1）求证：EG=CG；

（2）将图①中△BEF绕B点逆时针旋转45°，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；

（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论（均不要求证明）．

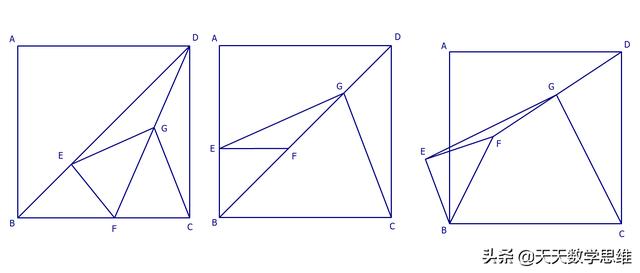
• 考点：旋转的性质；全等三角形的判定与性质；直角三角形斜边上的中线；正方形的性质。

• 分析：

• （1）利用直角三角形斜边上的中线等于斜边的一半，可证出CG=EG．

（2）结论仍然成立，连接AG，过G点 作GM⊥AB于M，再证明

（3）结论依然成立．很明显也有EG⊥CG．

解答：（1）证明：在Rt△FCD中，

∵G为DF的中点，

∴CG=FD.2，

同理，在Rt△DEF中，

EG=FD/2，

∴CG=EG．

（2）解：（1）中结论仍然成立，即EG=CG．

证法一：连接AG，过G点作GM⊥AE于M，

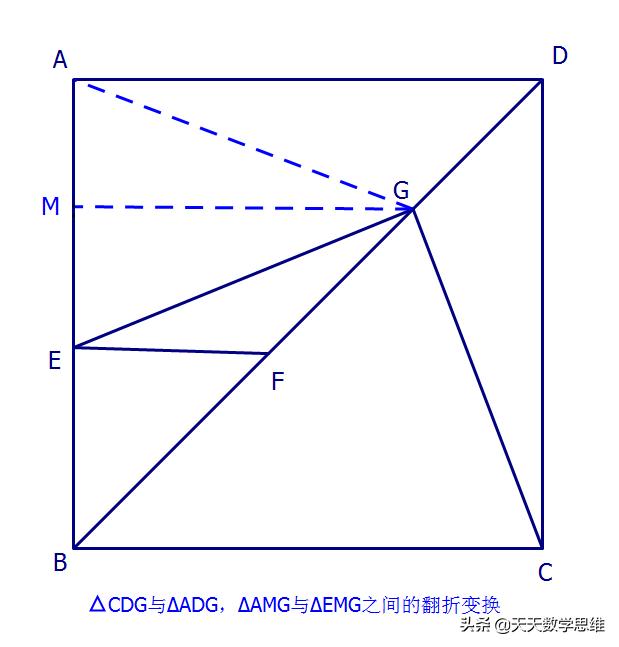
在△DAG与△DCG中，

∵AD=CD，∠ADG=∠CDG，DG=DG，

∴△DAG≌△DCG（SAS），

∴AG=CG；

∵FE⊥AE,又G是FD中点，

GM是直角梯形AEFD中位线

∴M是AE中点

GM是AE的垂直平分线

∴AG=EG，

∴EG=CG；

证法二：延长CG至M，使MG=CG，

连接MF，ME，EC，

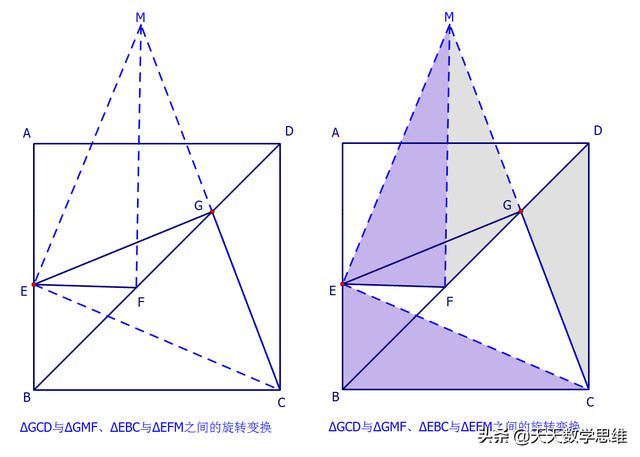
在△GCD与△GMF中，

∵FG=DG,∠MGF=∠CGD,MG=CG，

∴△DCG≌△FMG(SAS)．

∴MF=CD，∠FMG=∠DCG

∴MF//CD//AB，

∴EF⊥MF．

在Rt△EFM与Rt△EBC中，

∵MF=CB，EF=BE，

∴△MFE≌△CBE(HL)

∴∠MEF=∠CEB．

∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°，

∴△MEC为直角三角形．

∵MG=CG，

∴EG=MC/2，

∴EG=CG．

（3）解：（1）中的结论仍然成立．

即EG=CG．其他的结论还有：EG⊥CG．

小结：本题利用了直角三角形斜边上的中线等于斜边的一半的性质、梯形中位线、全等三角形的判定和性质．难度不是很大，注意其中的翻折和旋转。

例2．如图1，点P是线段MN的中点．

（1）请你利用图1画一对以点P为对称中心的全等三角形；

（2）请你参考这个作全等三角形的方法，解答下列问题：

①如图2，在Rt△ABC中，∠BAC=90°，AB＞AC，点D是BC边中点，过D作射线交AB于E，交CA延长线于F，请猜想∠F等于多少度时，BE=CF（直接写出结果，不必证明）；

②如图3，在△ABC中，如果∠BAC不是直角，而（1）中的其他条件不变，若BE=CF的结论仍然成立，请写出△AEF必须满足的条件，并加以证明．

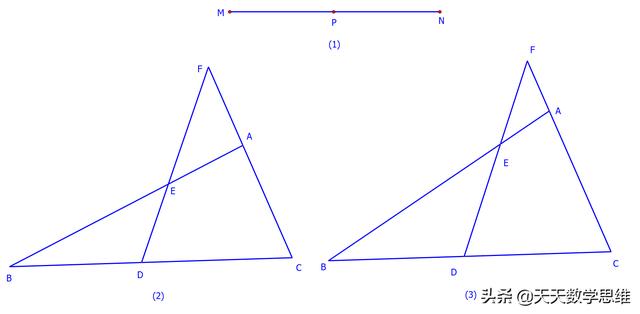
• 考点：作图；全等三角形的判定；等腰三角形的判定。

• 分析：

（1）画一对中心对称的全等三角形；

（2）当BE=CF时，∠F的结论成立；第2小题需要用到辅助线的帮助．有中点所以我们考虑将三角形绕该点旋转。延长FD到点G，使得FD=GD，连接BG，证明△DCF≌△DBG后推出∠F=∠G，CF=BG，从而证明BE=CF．

解答：解：（1）略

（2）①∠F=45°时，BE=CF．

②若BE=CF的结论仍然成立，

则AE=AF，△AEF是等腰三角形．

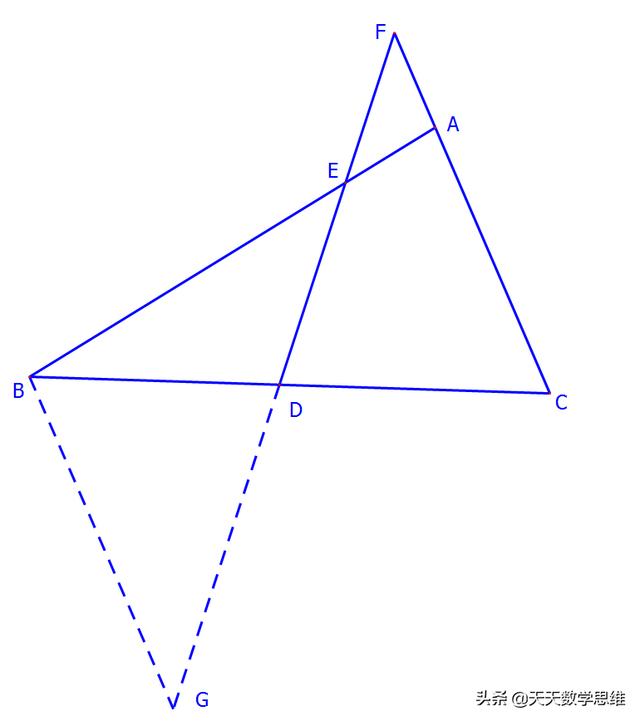
证明：延长FD到点G，使得FD=GD，连接BG．

∵点D是BC边中点，

∴DC=DB

在△DCF和△DBG中

DC＝DB ，∠CDF=∠BDG，DF＝DG

∴△DCF≌△DBG．（SAS）

∴∠F=∠G，CF=BG

当△AEF是等腰三角形，AE=AF时，

∠F=∠AEF，

∵∠AEF=BED，

∴∠BED=∠G．

∴BE=BG．

∴BE=CF．

点评：本题涉及全等三角形，等腰梯形的相关性质和判定，图（1）是作为思路的引导，但有时候不会给出这样的引导，需要运用中点相关的旋转去自己发现，本题考查学生的作图能力，为综合题型，难度适中．