广东省初中数学学业水平考试（1）第25题（压轴题）

25.如图，已知顶点为C（0，-3）的抛物线y=ax2+b（a≠0）与x轴交于A，B两点，直线y=x+m过顶点C和点B.

（1）求m的值；

（2）求函数y=ax2+b（a≠0）的解析式；

（3）抛物线上是否存在点M，使得∠MCB=15°？若存在，求出点M的坐标；若不存在，请说明理由.

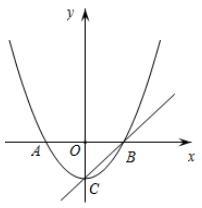
这是一道关于二次函数的题目，第1,2小问是比较常规的题型，所以在这里只提供解题思路和答案，第3小问才是我们要讨论的重点。

解题思路：

（1）直线y=x+m，过点C，直接把C的坐标代入直线解析式，就可以求出m的值。

（2）根据（1）求出的直线解析式，令y=0，求出B的横坐标，得到B点坐标。然后把B、C坐标代入抛物线方程，求出参数a、b,即可得到抛物线的解析式。

（3）分M在B上方和下方两种情况.若M在B上方，则∠ODC=∠DBC+∠DCB=60°，利用三角函数的知识求出OD，则可得点D的坐标，由此利用待定系数法求出直线CD的解析式，与抛物线解析式连立，即可得点M的坐标，同理求出M在B下方时M的坐标，即可完成解答.

解：（1）因为直线过点C，将C（0，-3）代入y=x+m，得 -3=0+m,解得m=-3.

将y=0代入y=x-3，得x=3，

∴点B的坐标为（3，0）.

将（0，-3），（3，0）代入y=ax2+b中，可得{b=−39a+b=0，

解得 a=1/3，b=-3

所以二次函数的解析式为y=1/3x^2-3.

第3小题，我先提供一种当时自己在做这道题目的解答过程，请大家看看有没有什么问题？

看起来好像没问题，但是二次函数学得好的同学应该会有一个疑问，你做的这种情况是点M在x轴的上方，如果点M在X轴的下方，那情况还是一样的？从这道题来看，情况是不一样的，所以我们必须分两种情况来讨论，第一种情况就如上面所说，现在我们来想想，如果点M在X轴下面，又该如何解答呢：

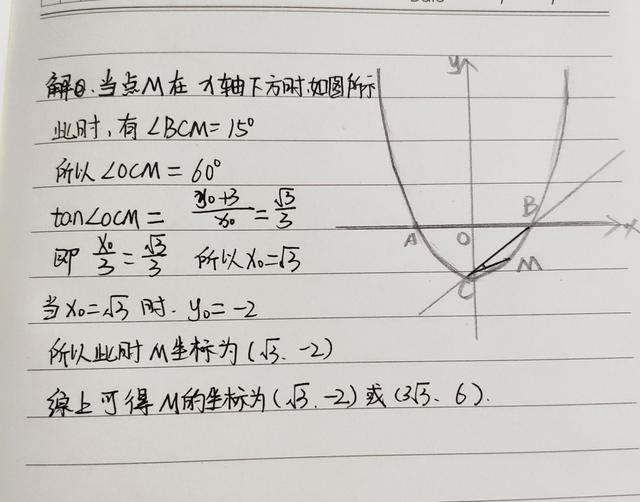
第3小题标准答案：

（3）存在，分以下两种情况：

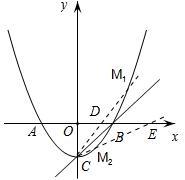
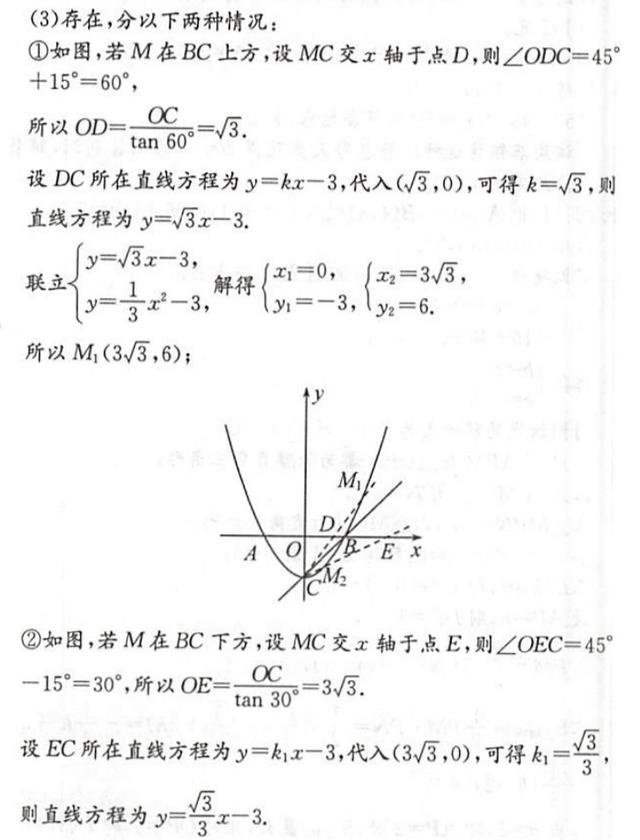
所以从这道题，就要吸取教训，以后在做二次函数动点题目的时候要多留意一下，反之漏掉可能出现的情况，今天的分享就先到这里啦，下次再见。