中考数学：判定两直线平行的六种方法

在几何题的证明过程中，经常需要判定两直线平行。而直线平行的判定方法有很多，我们要根据图形的特征和已知条件灵活选择方法。今天我们将介绍六种判定两直线平行的方法。

方法一：利用平行线的定义

例1：下面几种说法中，正确的是（ ）

A.同一平面内不相交的两条线段平行

B.同一平面内不相交的两条射线平行

C.同一平面内不相交的两条直线平行

D.以上三种说法都不正确

答案：C

方法二：利用“同位角相等，两直线平行”

例2：如图，已知∠ABC＝∠ACB，∠1＝∠2，∠3＝∠F，试判断EC与DF是否平行，并说明理由．

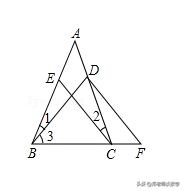
例2图

【分析】因为∠ABC＝∠ACB，∠1＝∠2，所以∠3＝∠ECB，又因为∠3＝∠F，则有∠ECB＝∠F，同位角相等，故EC∥DF，据此解答即可．

【解答】解：EC∥DF

理由：

∵∠ABC＝∠ACB，∠1＝∠2

∴∠3＝∠ECB

∵∠3＝∠F

∴∠ECB＝∠F

∴EC∥DF（同位角相等，两直线平行）

【点评】本题考查了平行线的判定，解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角进行解答．

方法三：“利用内错角相等，两直线平行”

例3：如图，∠ABC＝∠BCD，∠1＝∠2，求证：BE∥CF．

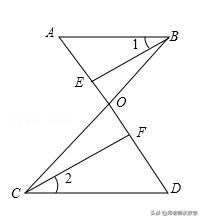
例3图

【分析】求出∠EBC＝∠BCF，根据平行线的判定得出即可．

【解答】证明：∵∠ABC＝∠BCD，∠1＝∠2，

∴∠ABC﹣∠1＝∠BCD﹣∠2，

∴∠EBC＝∠BCF，

∴BE∥CF（内错角相等，两直线平行）

【点评】本题考查了平行线的判定定理的应用，能运用平行线的判定定理进行推理是解此题的关键，注意：内错角相等，两直线平行．

方法四：利用“同旁内角互补，两直线平行”

例4：如图，点E在线段DF上，点B在线段AC上，若∠1＝∠2，3＝∠4，则∠A＝∠F．请将下面证明过程或理由补充完整．

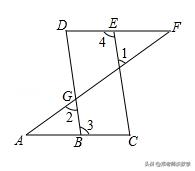
例4图

证明∵∠1＝∠2（已知），∠2＝∠DGF（　对顶角相等　），

∴∠1＝∠DGF，

∴BD∥CE（　同位角相等，两直线平行　），

∴∠3+∠C＝180°（　两直线平行，同旁内角互补　）；

又∵∠3＝∠4（已知），

∴∠4+∠C＝180°，

∴　DF　∥　AC　（同旁内角互补，两直线平行），

∴∠A＝∠F（　两直线平行，内错角相等　）．

方法五：“利用平行于同一条直线的两直线平行”

例5：如图，已知∠B＝∠CDF，∠E+∠ECD＝180°，证明：AB∥EF．

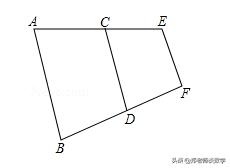
例5图

证明：∵∠B＝∠CDF

∴　AB　∥　CD　（同位角相等，两直线平行）

∵∠E+∠ECD＝180°

∴　CD　∥　EF　（同旁内角互补，两直线平行）

∴AB∥EF（平行于同一条直线的两直线互相平行）

方法六：利用“垂直于同一条直线的两直线平行”

例6：如图，在三角形ABC中，CE⊥AB于E，DF⊥AB于F，AC∥ED，CE是∠ACB的平分线，试比较∠EDF与∠BDF的大小，并说明理由．

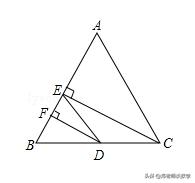
例6图

【分析】想办法证明∠FDE＝∠DEC＝∠ACE，∠BDF＝∠BCE，再根据角平分线的性质即可解决问题．

【解答】解：∠EDF＝∠BDF．理由如下：

∵AC∥ED，

∴∠ACE＝∠DEC．

∵CE⊥AB，DF⊥AB，

∴DF∥CE（垂直于同一条直线的两直线平行）

∴∠BDF＝∠BCE，∠FDE＝∠DEC，

∴∠FDE＝∠ACE，

∵CE平分∠ACB，

∴∠ECB＝∠ACE，

∴∠EDF＝∠BDF．

【点评】本题考查平行线的性质、角平分线的定义、垂线的定义等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．