高中数学线性规划应用题解题策略

例1 某企业生产甲、乙两种产品，已知生产每吨甲产品要用A原料3吨、B原料2吨；生产每吨乙产品要用A原料1吨、B原料3吨。销售每吨甲产品可获得利润5万元，每吨乙产品可获得利润3万元，该企业在一个生产周期内消耗A原料不超过13吨，B原料不超过18吨，那么该企业可获得最大利润是

A. 12万元 B. 20万元 C. 25万元 D. 27万元

点评：

此类题需要先建模（设未知数，列约束条件，列目标函数），后求解。此类问题对未知数没有整数要求，故求解方法同一般的线性规划问题一样，用技巧也行，用基本方法也行（建议多练练基本方法）。

第二类：未知数需要满足整数问题，并且交点坐标不是整数的情况

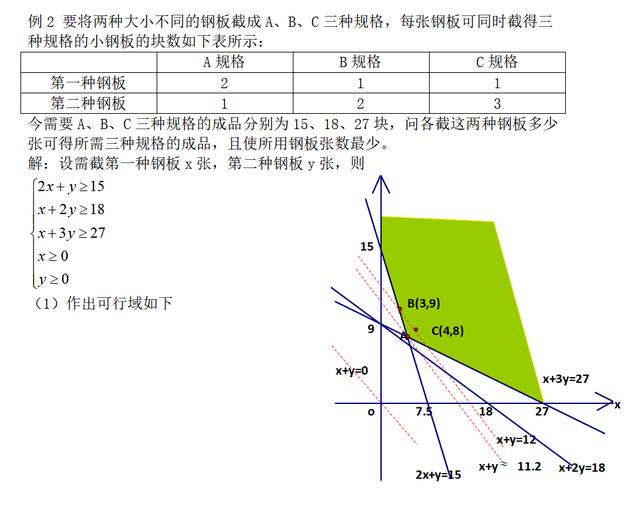
（2）目标函数为z=x+y，即y= -x+z，可知当直线截距取最小值时，目标函数取得最小值

（3）作直线即y= -x

（4）平移直线，直线经过直线x+3y=27和直线2x+y=15的交点A（18/5,39/5）时，截距最小

（5）z =x+y=57/5=11.4

由于18/5和39/5都不是整数，而最优解(x,y)中，x、y必须都是整数，所以，可行域内点A（18/5,39/5）不是最优解

（6）调整（解决此类问题重点）

由于x、y必须都是整数，所以将平行线继续向右平移到x+y=12

由x+y=12且2x+y=15,得x+y=12与可行域左边界的交点B（3，9） 由

得到x+y=12与可行域右边界的交点D（9/2,15/2），在BD线段上的整点均是本题的最优解，所以，B（3，9），C（4，8）都是最优解。

（注：若x+y=12时仍无整解出现，则需将平行线继续向右平移到x+y=13按上面方法寻找即可）

总结：

对于线性规划实际问题需求整数解时，需要对平行线进行移动，结合图像进行分析和计算，直到求出最小正整数解为止。同时此类题也需要同学们对基本方法的掌握，如果只掌握了交点法那种技巧，那么遇到此类题就束手无策了。