精典考题透视

例.如图，已知直线y=1/2x与双曲线y=k/x(k>0)交于A，B两点，且点A的横坐标为4.

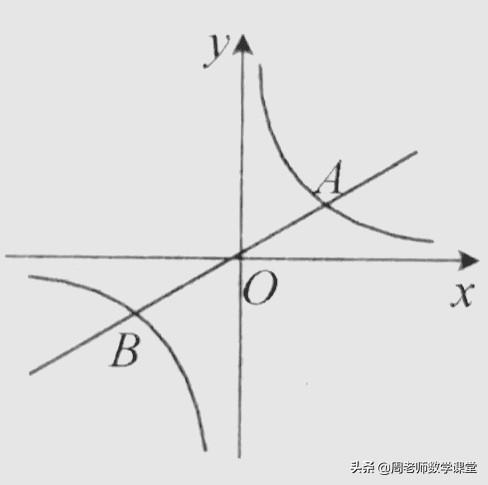
⑴ 求k的值；

⑵ 若双曲线y=k/x(k>0)上一点C的纵坐标为8，求△AOC的面积；

⑶ 过原点O的另一条直线l交双曲线y=k/x(k>0)于P，Q两点(P点在第一象限)，若由点A，B，P，Q为顶点组成的四边形面积为24，求点P的坐标。

解析：(1)∵点A的横坐标为4，

∴当x=4时，y=1/2×4=2.

∴点A的坐标为(4，2).

又∵点A是直线y=1/2x与双曲线y=k/x(k>0)的交点，

∴2=k/4.

∴k=8.

⑵解：如图，

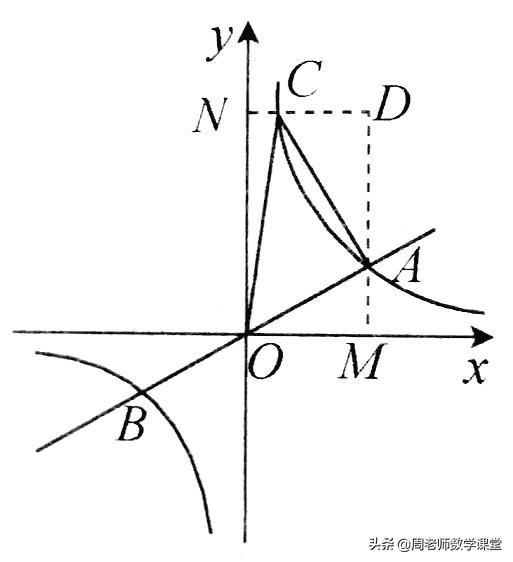
∵点C在双曲线上，即当y=8时，x=1.

∴点C的坐标为(1，8)，

过点A，C分别作x轴、y轴的垂线，垂足为M，N，两垂线交于D，得矩形ONDM，且M(4，0)，N(0，8).

∵S矩形ONDM=OM·ON=32.

S△ONC=1/2NC·ON=4，

S△CDA=1/2CD·AD=9，

S△OAM=1/2OM·AM=4，

∴S△AOC=S矩形ONDM-S△ONC-S△CDA-

S△OAM=15.

⑶如图，

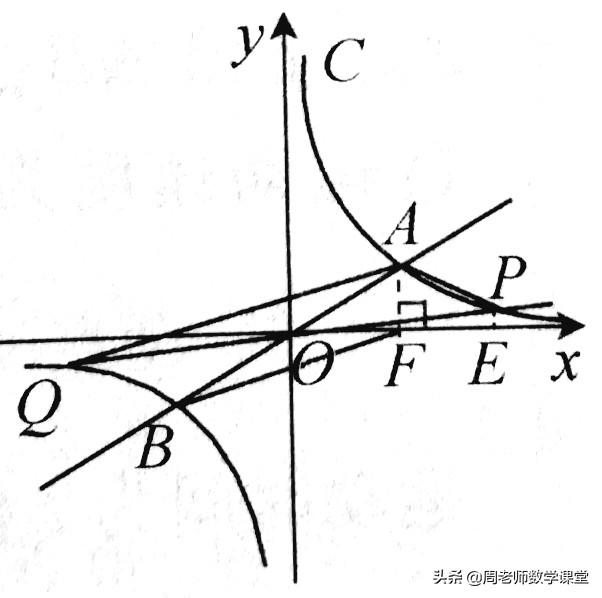
∵反比例函数图象是关于原点O的中心对称图形

∴OP=OQ，OA=OB.

∴四边形APBQ是平行四边形.

∴S△POA=1/4 S平行四边形APBQ=1/4×24=6.

设点P的横坐标为m(m>0且m≠4)，则P(m，8/m).

过点P，A分别作x轴的垂线，垂足为E，F.

∵点P，A在双曲线上，

∴S△POE∴S△POE=S△AOF=4.

若0<m<4，如图，

∵S△POE +S梯形PEFA=S△POA +S△AOF，

∴S梯形PEFA=S△POA=6.

∴1/2·(2+8/m)·(4-m)=6.

解得m1=2，m2=-8(含去)，

∴P点的坐标为(2，4).

若m>4，如图.

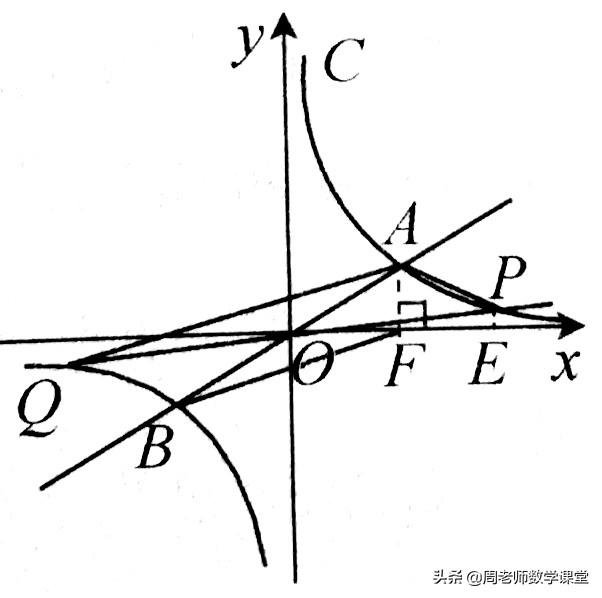
同理.S△AOF+S梯形AFEP=S△POA+S△POE，

∴S梯形AFEP=S△POA=6.

∴1/2·(2+2)·(m-4)=6.

解得m1=8，m2=-2(舍去).

∴P点的坐标为(8，1).

综上∴点P的坐标是(2，4)或(8，1).

思想小结

数形结合思想把“数”这个抽象的概念与较为直观的“形”紧密地联系起来，产生思维的火花，从而达到简化问题、解决问题的目的。数形结合思想包含了转化、配方、分类讨论、方程等数学思想方法，可见数形结合思想方法是数学中极具综合性的思想方法。

数形结合思想方法就是要对一个问题尽可能做到全方位、多角度地认识，这样，一方面可以加强思维的深刻性，另一方面又可以开拓思路，培养思维的灵活性。数学的题型是千变万化，同学们在学习中要善于归纳和总结，把数形结合思想用好用活，提高我们的学习能力。