《平面直角坐标系》单元练习

一、选择题（每小题3分，共 30 分）

1. 已知点P（2a﹣5，a+2）在第二象限，则符合条件的a的所有整数的和的立方根是（ ）

A. 1

B. ﹣1

C. 0

D.2的3次方根

【答案】D

【解析】∵点P(2a−5，a+2)在第二象限，

解得：−2<a<52

符合条件的a的所有整数为−1，0，1，2，

∴−1+0+1+2=2，

∴2的立方根为D ，

故选：D.

2. 周末，小明与小文相约一起到游乐园去游玩，如图是他俩在微信中的一段对话：

第2题

根据上面两人的对话纪录，小文能从M超市走到游乐园门口的路线是（ ）

A. 向北直走700米，再向西直走300米

B. 向北直走300米，再向西直走700米

C. 向北直走500米，再向西直走200米

D. 向南直走500米，再向西直走200米

【答案】A

【解析】小文能从M超市走到游乐园门口的路线是：

向北直走700米，再向西直走300米。

故选：A.

3. 一个正方形在平面直角坐标系中三个顶点的坐标为（－2，－3），（－2，1），（2，1），则第四个顶点的坐标为（ ）

A. （2，2）

B. （3，2）

C. （2，－3）

D. （2，3）

【答案】C

【解析】已知正方形的两个顶点为（-2，-3），（-2，1），

可得正方形的边长为：1-（-3）=4，

再由第三个点的坐标为（2，1），

可求得第四个顶点的坐标为（2，-3），故选D.

点睛：本题考查了坐标与图形的性质，解决本题的关键是弄清当两个点的横坐标相等时，其两点之间的距离为纵坐标的差．

4. 点P（x，y），且xy＜0，则点P在（ ）

A. 第一象限或第二象限

B. 第一象限或第三象限

C. 第一象限或第四象限

D. 第二象限或第四象限

【答案】D

【解析】∴x，y异号，

当x>0时，y<0，即点的横坐标大于0，纵坐标小于0，点在第四象限；

当x<0时，y>0，则点的横坐标小于0，纵坐标大于0，点在第二象限。

故选：D.

5. 如图1，与图1中的三角形相比，图2中的三角形发生

的变化是（ ）

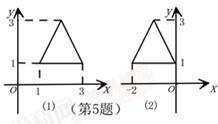
第5题

A. 向左平移3个单位长度

B. 向左平移1个单位长度

C. 向上平移3个单位长度

D. 向下平移1个单位长度

【答案】A

【解析】由图①到图②，点(1,1)平移到点(−2,1)，

点(3,1)平移到点(0,1)，都是向左平移3个单位，

∴图形平移规律为：向左平移3个单位。

故选A.

6. 如图3所示的象棋盘上，若帅位于点（1，－2）上，相位于点（3，－2）上，

则炮位于点（ ）

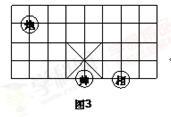
第6题

A. （1，－2）

B. （－2，1）

C. （－2，2）

D. （2，－2）

【答案】B

【解析】试题分析：首先根据题意得出坐标原点，然后求出炮所在的位置.

考点：平面直角坐标系

7. 若点M（x，y）的坐标满足x＋y＝0，则点M位于（ ）

A. 第二象限

B. 第一、三象限的夹角平分线上

C. 第四象限

D. 第二、四象限的夹角平分线上

【答案】D

【解析】∵x+y=0，

∴y=−x，

∴点M(x，y)位于第二、四象限的夹角平分线上。

故选：D.

8. 将△ABC的三个顶点的横坐标都加上－1，纵坐标不变，则所得图形与原图形的关系是（ ）

A. 将原图形向x轴的正方向平移了1个单位；

B. 将原图形向x轴的负方向平移了1个单位

C. 将原图形向y轴的正方向平移了1个单位

D. 将原图形向y轴的负方向平移了1个单位

【答案】B

【解析】∵将△ABC的三个顶点的横坐标都加上−1，纵坐标不变，

∴所得图形与原图形的位置关系是△ABC向x轴的负方向平移1个单位。

故选：B.

9. 在坐标系中，已知A（2，0），B（－3，－4），C（0，0），则△ABC的面积为（ ）

A. 4

B. 6

C. 8

D. 3

【答案】A

【解析】由题意点B坐标的纵坐标的绝对值即为△ABC底边AC的高，

∴AC=|2−0|=2，

∴S△ABC=1/2×AC×|−4|= 1/2×2×4=4.

故选：A.

点睛：本题考查了三角形面积的计算，确定三角形ABC的底边AC，以及该底边上的高点B的纵坐标即可求得.

10. 点P（x－1，x＋1）不可能在（ ）

A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

【答案】D

【解析】本题可以转化为不等式组的问题，看下列不等式组哪个无解，

（1） x-1＞0, x+1＞0 ，解得x＞1，故x-1＞0，x+1＞0，点在第一象限；

（2） x-1＜0 ,x+1＜0 ，解得x＜-1，故x-1＜0，x+1＜0，点在第三象限；

（3） x-1＞0 ,x+1＜0 ，无解；

（4） x-1＜0 ,x+1＞0 ，解得-1＜x＜1，故x-1＜0，x+1＞0，点在第二象限．

故点P不能在第四象限，故选D．