“将军饮马”模型在实际解决最短路径和动点问题的应用

唐朝诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河”诗中隐含着一个有趣的数学问题．

如图所示，诗中将军在观望烽火之后从山脚下的A点出发，走到河边饮马后再到B点宿营．请问怎样走才能使总的路程最短？这就是所谓的“将军饮马”问题。

实际上，我们将问题再进一步画图：

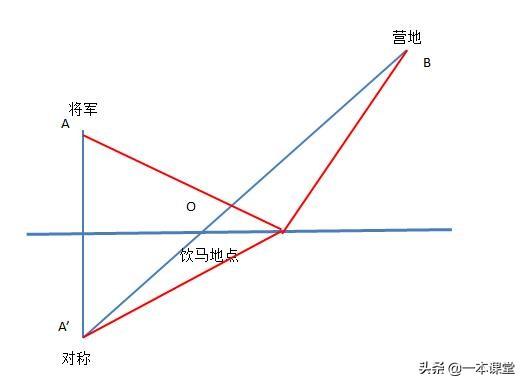
图中所示O点便为最佳的饮马地点，原因在于从A到O和从A’到O距离相等，而两点间距离最短，所以A’B能取的最短值便是（红色长于蓝色）。

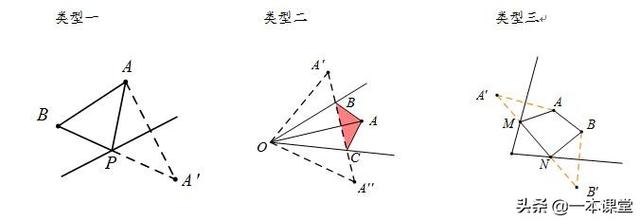
这只是"将军饮马"问题的一种形式，它还有多种变化（在直线上找一点满足下列条件）：

（1）PA+PB最小

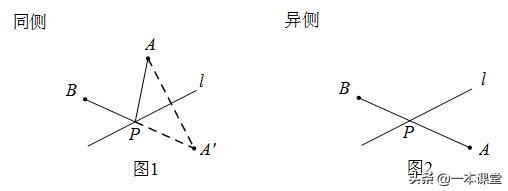
（2）PA-PB最小

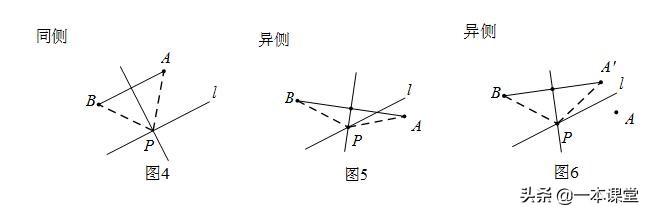
（2）PA-PB最大

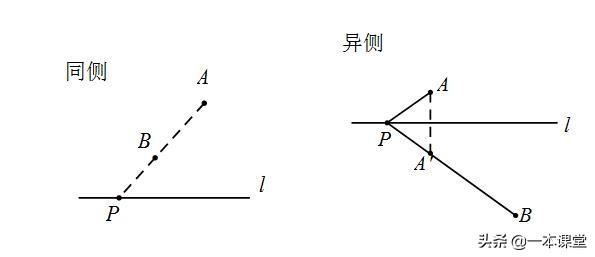
（4）周长最短

（5）“过河”最短距离（注意河宽）

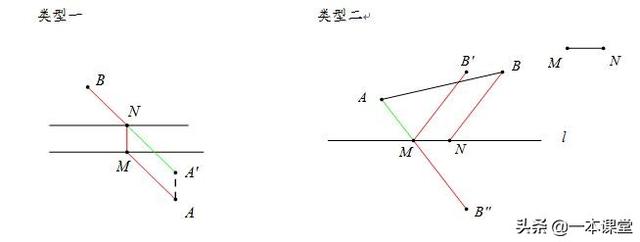
（6）线段和最小（实线）

（7）坐标系中的应用

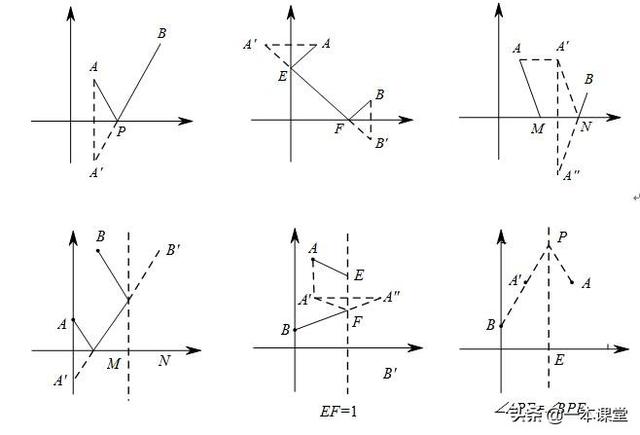
把模型简单进行举例：

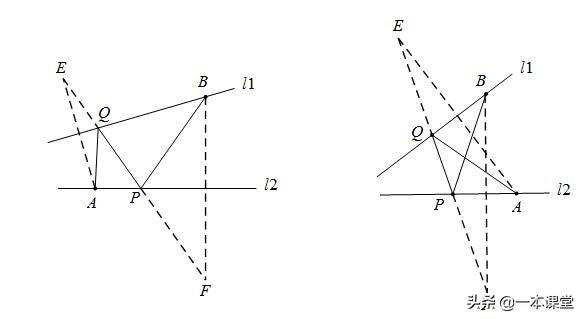
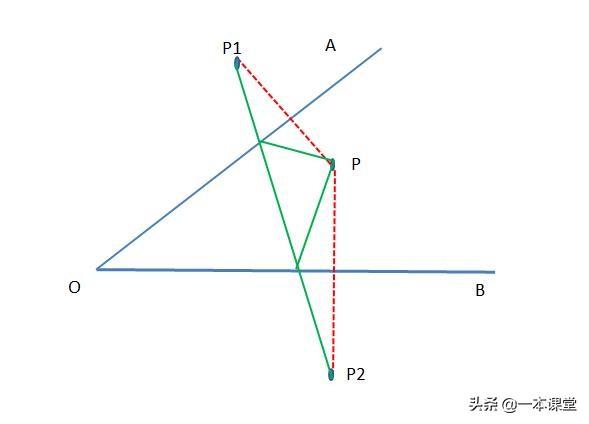
1、如图，点 P 在锐角∠AOB 的内部，在 OB 边上求作一点 D，在 OA 边上求作一点 C，使△ PCD 的周长最小。

思路：做点P关于直线OA, OB的对称点P1, P2，P1P2与直线OA、OB的交点为所求点C、D，PCD的周长最小值为P1P2的长。

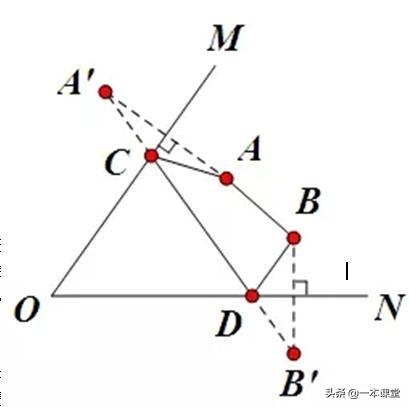
2、在∠MON的内部有点A和点B，在OM上找一点C，在ON上找一点D，使得四边形ABCD周长最短．

思路：作点A关于OM的对称点A’，作点B关于ON的对称点B’ ，连接A’ B’，与OM交于点C，与ON交于点D，连接AC，BD，AB，四边形ABCD即为所求．

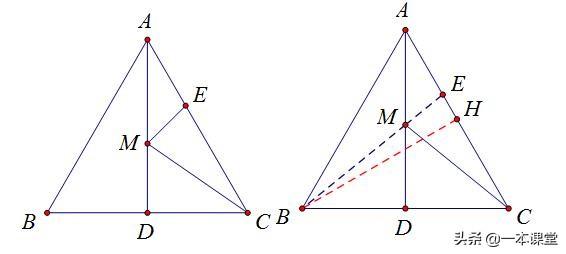
3、如图，在等边△ABC中，AB = 6，AD⊥BC，E是AC上的一点，M是AD上的一点，且AE = 2，求EM+EC的最小值

思路：同样找C关于AD的对称点，实际上即为B，

实际上在中考试题中也经常出现类似题目，有兴趣的可以找一下。