初中数学：“一线三等角”模型速解一道反比例函数题

在初中几何里，“一线三等角”相似模型，非常重要。我常常跟学生说一句话“见到直角，不妨想想构造一线三等角”从而得到相似来解题。本文选取一道比较简单但是不失精彩的反比例函数小题，巧用这个模型，再配合反比例函数的几何性质（面积与K的关系），从而达到快速解题的目的。如图：

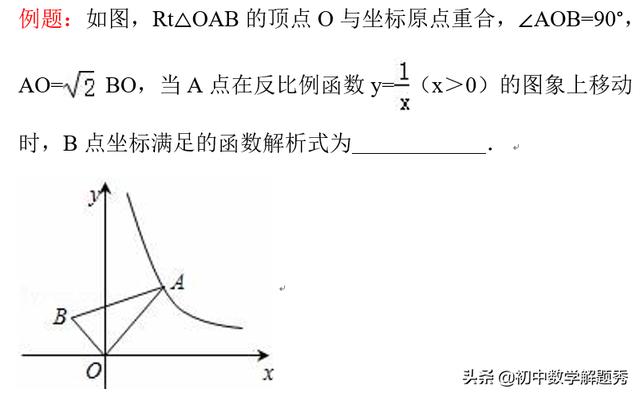
看完这个题目，可以知道：A在反比例函数y=1/x上，∠AOB=90°，直角边OA:OB=√2:1.根据“种瓜得瓜，种豆得豆”的数学思想，可以“预感”B点也在反比例函数上，即B的轨迹也应该是“遗传”A点的形状信息！但是怎样求点B的函数解析式呢？

结合出现“直角”+“反比例函数”的双重“信号”，我们不妨构造“一线三等角”+“反比例函数面积性质”来快速解题。先来看看模型，如图：

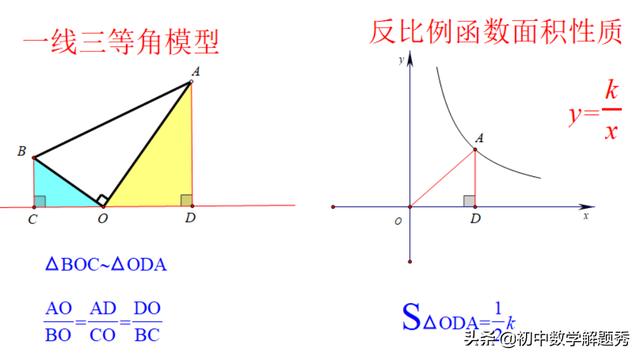
经过分析，可以知道如果把上述两个模型“整”到一起，再借助相似三角形面积比等于相似比的平方，本题相似比是边OA:OB=√2:1，而垂轴直角三角形面积恰恰又是k的一半，从而兵不血刃，迅速解题！如图：

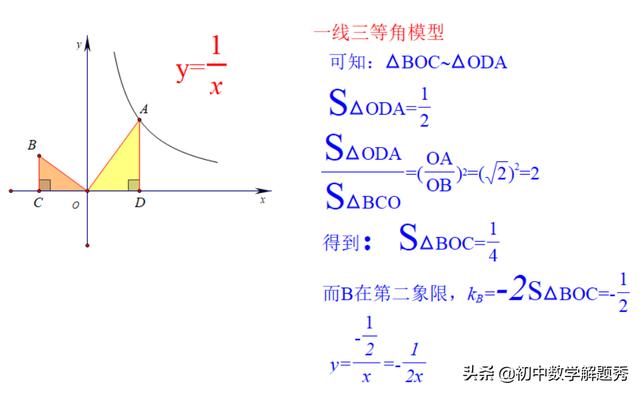
本题通过构造“一线三等角”+“反比例函数面积性质”+相似三角形面积比，快速解题，思维紧凑，环环相扣，小题大能量，我很喜欢。当然了，本题还要理解B点只能在第二象限，所以还要写清自变量取值范围。