三角函数最值问题的分类探究

一、引言

三角函数最值问题处在代数、三角、几何等知识的交汇处，解法灵活多变，能力要求高，是高考的常考点。在求解时，若能根据题目特征，合理选择方法则可以快速解题。

二、分类呈现

A、y=asinx+b型

题中仅含正弦或余弦一种，且次数为1，这一类问题相对比较简单，通常求解方法是将正弦或余弦函数转化成一次函数，然后利用三角函数的有界性进行解决。

评注：将三角函数转化为在一定区间上求代数函数最值是常用的方法，还可以尝试运用数形结合，转化为斜率问题等方法来进行求解。

B、化成y=Asin（ωx+φ）的形式

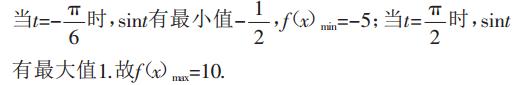
评注：此类题目看起来较为复杂，难以厘清思路，巧妙变形转化后，再结合三角函数有界性进行求解，问题则迎刃而解.需要说明的是：若函数是条件函数，则常需利用三角函数的图像来解题。

评注：题目看起来较为复杂，但厘清思路后发现，此题的关键：把问题化归为f（x）=Asin（ωx+φ）+k的形式，但如果已附加x的取值范围，通过图像来解决为最佳办法。

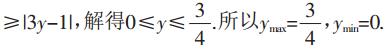
评注：通常利用辅助角公式及利用正（余）弦函数的有界性，转化为以函数y为主元的不等式.另外，可用万能公式、圆的参数方程和斜率公式求解。

C、二次函数型

D、对勾函数形式型

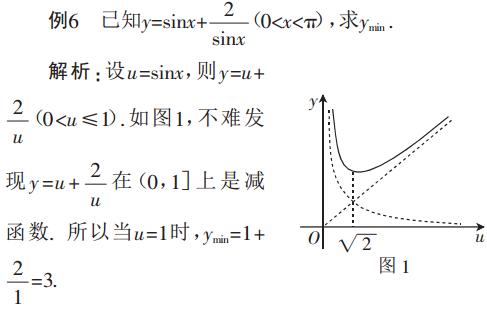
E、y=asinxcosx+b(sinx±cosx)+c型

评注：sinα+cosα，sinα-cosα，sinαcosα相互制约与关联.知其一，则能够求出其二，令t=sinx-cosx换元后，则可使用配方法、函数的单调性、重要不等式等法去求函数的最值。

三、结语

总结规律，摸索经验.在解决三角函数的最值相关问题时，常会出现一些忽视题设条件、概念模糊、方法不当等问题，导致求解困难.基于此，在解决相关问题时，要注意三角函数的变形方向、正(余)弦的有界性、灵活选择方法、多多练习，确保考虑周全，准确无误，答题精准。