初中数学：解一道“阿波罗尼斯圆”最值问题

在初中数学中，有一类几何动点最值问题，学生普遍感到“害怕”。它就是“阿波罗尼斯圆”问题：平面上有A，B两点，则所有满足PA/PB=k且不等于1的点P的轨迹是一个以定比m：n内分和外分定线段AB的两个分点的连线为直径的圆，这个轨迹最早由古希腊数学家阿波罗尼斯发现，故也称阿氏圆。

估计读完这个概念，你就彻底崩溃啦！别怕，有我在！我来给你举例科普一下。

例题：圆O的半径为3，A(0,6) ，B(8,0)，P是圆上一个动点，求 PB+1/2PA的最小值____

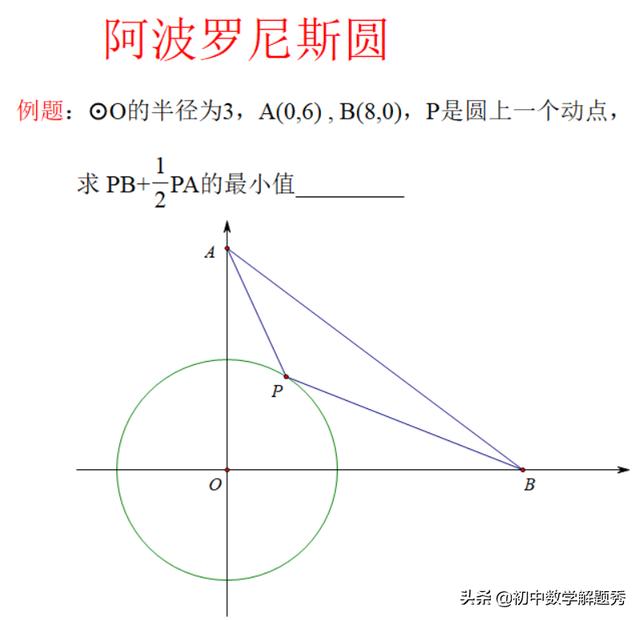
显然这个题最“讨厌”的地方就是1/2PA，我们要想办法把它转化为“一条线段”和PB建立起符合之前熟悉的动点最值模型。解决阿波罗尼斯圆问题的通法是构造相似转化问题。

连接PO，利用相似比OA:OP=2,构造OP:OC=2,从而得到相似(SAS相似模型)，如图：

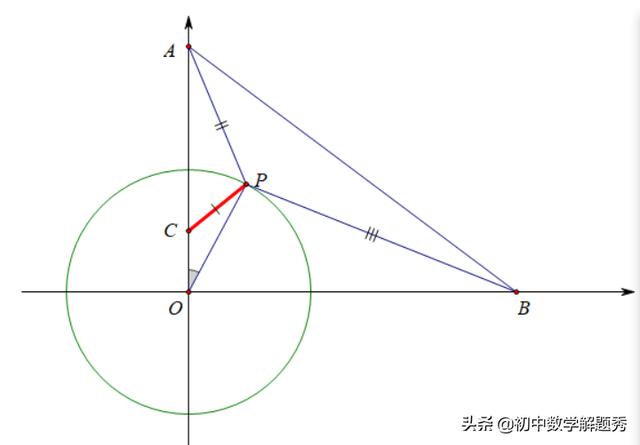
由OA:OP=OP:OC=2，∠AOP=∠POC,得△AOP∽△POC，继而可得1/2PA=PC,问题得以转化： PB+1/2PA=PC+PB.问题做到这一步，我想大家都会做了：两个点C和B都是定点，而P是动点，PC+PB的最小值就是线段BC的值（依据：两点之间线段最短）。显然C,B两个点的坐标可知：C(0,1.5),B(8,0)，BC=√265/2.而P点的位置就是线段BC和圆的交点，如图：

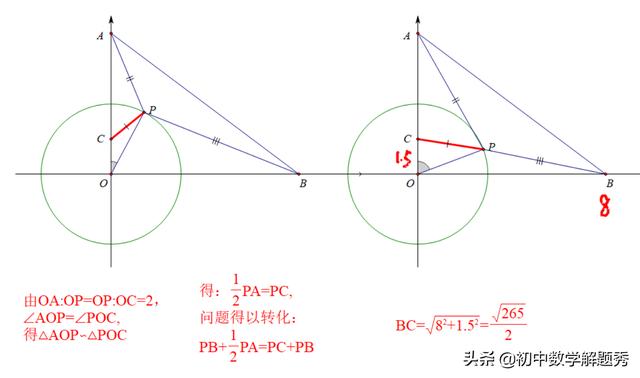
上述过程，简单地给大家举个例子，科普一下“阿波罗尼斯圆”问题，大家感觉如何？能不能消除一点心中的恐惧？几何就是“难了不会，会了不难”，而阿波罗尼斯圆问题，你只要学会了构造相似转化，就可以解决问题了。

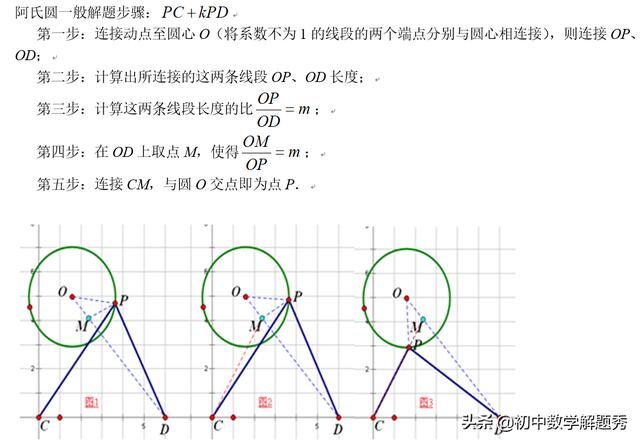
最后给大家总结一下“阿波罗尼斯圆”的解题套路，大家好好体会，对照模型：绝技在手，天下我有！如图：