中考复习：分类讨论思想在等腰三角形中的应用

分类讨论思想是解题的一种常用方法，在等腰三角形中，往往会遇到条件或结论不唯一的情况。此时就需要进行分类讨论。通过正确地分类讨论，可以使复杂的问题得到清晰、完整、严密的解答。其解题策略是：先分类，再画图，最后计算。下面我们将进行举例说明。

应用一：当顶角或底角不确定时，分类讨论

例1：若等腰三角形中有一个角等于40°，则这个等腰三角形顶角的度数为（ ）

A．40° B．100° C．40°或100° D．40°或70°

【分析】由等腰三角形中有一个角等于40°，可分别从①若40°为顶角与②若40°为底角去分析求解即可求得答案．

【解答】解：∵等腰三角形中有一个角等于40°，

∴①若40°为顶角，则这个等腰三角形的顶角的度数为40°；

②若40°为底角，则这个等腰三角形的顶角的度数为：180°﹣40°×2＝100°．

∴这个等腰三角形的顶角的度数为：40°或100°．

故选：C．

【点评】此题考查了等腰三角形的性质．此题比较简单，解题的关键是掌握等边对等角的知识，掌握分类讨论思想的应用．

应用二：当底和腰不确定时，分类讨论

例2：已知一个等腰三角形的两边长分别是2和4，则该等腰三角形的周长为（ ）

A．8或10 B．8 C．10 D．6或12

【分析】分2是腰长与底边长两种情况讨论求解．

【解答】解：①2是腰长时，三角形的三边分别为2、2、4，

∵2+2＝4，∴不能组成三角形，

②2是底边时，三角形的三边分别为2、4、4，

能组成三角形，

周长＝2+4+4＝10，

综上所述，它的周长是10．

故选：C．

【点评】本题考查了等腰三角形的性质，难点在于要分情况讨论并利用三角形的三边关系进行判定．

例3：已知等腰三角形的两边长分别是6cm和10cm，求这个等腰三角形的周长。

【分析】根据等腰三角形的性质，分两种情况：①当腰长为6cm时，②当腰长为10cm时，解答出即可；

【解答】解：根据题意，

①当腰长为6cm时，周长＝6+6+10＝22（cm）；

②当腰长为10cm时，周长＝10+10+6＝26（cm）．

故答案为：22或26．

【点评】本题主要考查了等腰三角形的性质定理，本题重点是要分两种情况解答．

例4：等腰三角形的两边长分别是a和b，且满足|a﹣1|+（2a+3b﹣11）²＝0，这个等腰三角形的周长．

【分析】根据绝对值及偶次方的非负性结合|a﹣1|+（2a+3b﹣11）²＝0即可求出a、b的值，分a为腰长及b为腰长两种情况考虑：当a为腰长时，另一腰长为1，由三角形的三边关系可知此种情况不存在；当b为腰长时，另一腰长为3，根据三角形的周长公式即可求出结论．综上即可得出结论．

【解答】解：∵|a﹣1|≥0，（2a+3b﹣11）2≥0，且|a﹣1|+（2a+3b﹣11）²＝0，

∴a﹣1=0，2a+3b﹣11=0

解得：a=1，b=3

①当a为腰长时，另一腰长为1，

∵1+1＜3，

∴不符合三角形三边关系；

②当b为腰长时，另一腰长为3，

此时三角形的周长为3+3+1＝7．

综上所述，这个等腰三角形的周长为7．

【点评】本题考查了等腰三角形的性质、偶次方（绝对值）的非负性、三角形的三边关系以及三角形的周长，根据绝对值及偶次方的非负性结合|a﹣1|+（2a+3b﹣11）²＝0求出a、b的值是解题的关键．

应用三：当等腰三角形的形状不确定时，分类讨论

例5：等腰三角形一腰上的高与另一边的夹角为50°，求顶角的度数.

【分析】由于本题已知中没有明确指出等腰三角形是锐角三角形还是钝角三角形，因此要分情况讨论．

【解答】解：△ABC是等腰三角形，且∠BAC为顶角，CD是腰AB的高．

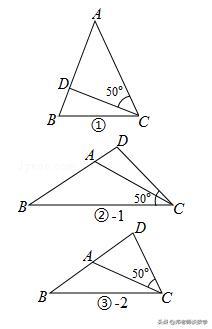
（1）当等腰三角形是锐角三角形时，如图①；

∵∠ACD＝50°，

∴∠BAC＝90°﹣∠ACD＝40°；

（2）当等腰三角形是钝角三角形时；

一、如图②﹣1；

当∠BCD＝50°时，∠B＝40°；

∴∠BAC＝180°﹣2∠B＝100°；

二、如图②﹣2；

当∠ACD＝50°时，∠CAD＝40°；

∴∠BAC＝180°﹣∠CAD＝140°；

故这个等腰三角形顶角的度数为：100°或140°或40°．

故答案为：100°或140°或40°．

应用四：由腰的垂直平分线引起的分类讨论

例6：在△ABC中，AB＝AC，AB的垂直平分线与AC所在直线相交所得的锐角为40°，求底角∠B的大小．

【分析】此题根据△ABC中∠A为锐角与钝角分为两种情况解答．

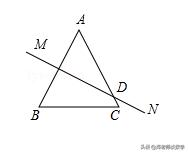
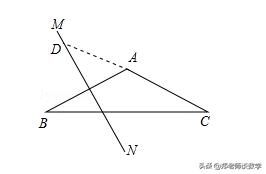
【点评】本题考查的是线段垂直平分线的性质以及等腰三角形的性质，此类题需要注意的是要分两种情况解答，考生在考虑问题时要全面．

应用五：由腰上的中线引起的分类讨论

例7：已知一个等腰三角形底边的长为5cm，一腰上的中线把其周长分成的两部分的差为3cm，则腰长为（ ）

A．2cm B．8cm C．2cm或8cm D．10cm

【分析】作出图形，根据三角形的中线的定义可得AD＝CD，然后求出两三角形的周长的差等于腰长与底边的差，然后分情况讨论求解即可．

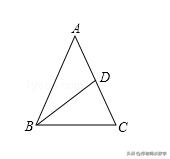
例7图

【解答】解：如图，∵BD是△ABC的中线，∴AD＝CD，

∴两三角形的周长的差等于腰长与底边的差，

∵BC＝5cm，

∴AB﹣5＝3或5﹣AB＝3，

解得AB＝8或AB＝2，

若AB＝8，则三角形的三边分别为8cm、8cm、5cm，能组成三角形，

若AB＝2，则三角形的三边分别为2cm、2cm、5cm，

∵2+2＝4＜5，∴不能组成三角形，

综上所述，三角形的腰长为8cm．

故选：B．

【点评】本题考查了等腰三角形的性质，三角形的中线，难点在于分情况讨论并利用三角形的三边关系判断是否能组成三角形．

应用六：点的位置不确定引起的分类讨论

例8：如图，在Rt△ABC中，∠ACB＝90°，AB＝2BC，在直线BC或AC上取一点P，使得△PAB为等腰三角形，则符合条件的点P共有（ ）

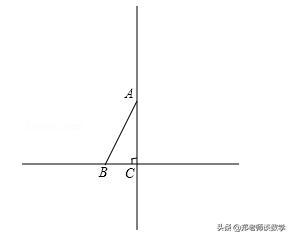
例8图

A．4个 B．5个 C．6个 D．7个

【分析】根据等腰三角形的判定，“在同一三角形中，有两条边相等的三角形是等腰三角形（简称：在同一三角形中，等边对等角）”分三种情况解答即可．

【解答】解：如图，

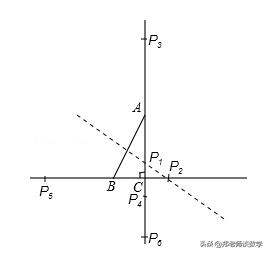
①AB的垂直平分线交AC一点P1（PA＝PB），交直线BC于点P2；

②以A为圆心，AB为半径画圆，交AC有二点P3，P4，交BC有一点P2，（此时AB＝AP）；

③以B为圆心，BA为半径画圆，交BC有二点P5，P2，交AC有一点P6（此时BP＝BA）．

2+（3﹣1）+（3﹣1）＝6，

∴符合条件的点有六个．

故选：C．

【点评】本题考查了等腰三角形的判定；构造等腰三角形时本着截取相同的线段就能作出等腰三角形来，思考要全面，做到不重不漏．