中考数学——一次函数的概念和正比例函数的图像

我们共同学习了函数的概念和表示方法。

我们知道了， 一般地，设在一个变化过程中有两个变量x与y，如果对于x在它允许取值范围内的每一个值，y都有唯一确定的值与它对应，那么我们就说x是自变量，y是x的函数。即为函数的定义。

今天，我们将学习一次函数概念及正比例函数的图像及性质。

首先一次函数的概念。

所谓一次函数即：若两个变量 x、y之间的关系可以表示成y=kx+b(k、b为常数，

k ≠ 0）的形式，则称 y是x的一次函数。（x为自变量，y为因变量。）

特别地， 当b=0时，一次函数y=kx(常数K≠ 0），次为特殊的一次函数，也叫做正比例函数。

正比例函数是一次函数的特殊形式！

例如函数关系式（1）y= - x - 4 （2）y=x^2 （3）y=2πx （4）y=1/x中（1）（3）是一次函数，不是正比例函数；（2）（4）不是一次函数，也不是正比例函数。

其次正比例函数的图像。

例1画出函数 y = 3x 的图象。通过列表，描点，连线得出如下图像。

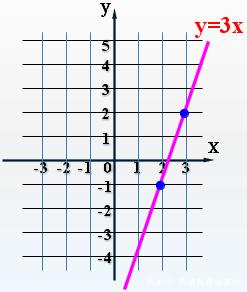
图1

结论：图像经过原点且过第一、三象限；图像自左向右上升：x的值增大，y的值也随之增大。

例2画函数 y=-3/2x 的图像

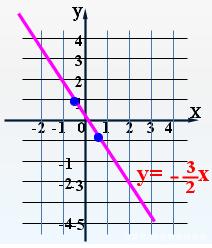
图2

结论：图像经过原点且过第二、四象限；图像自左向右下降：x的值增大，y的值减小。

例3:画函数 y =2x和y=-2x 的图像

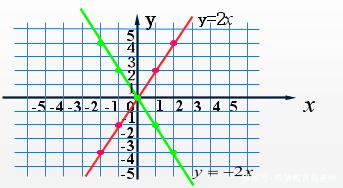
图3

结论：两图象都是经过原点的直线，函数y=2x的图象从左向右上升，经过第一三象限；函数y=-2x的图象从左向右下降，经过第二四象限。

例4画函数y=2x和函数y=-2/3x的函数图像，再找规律。

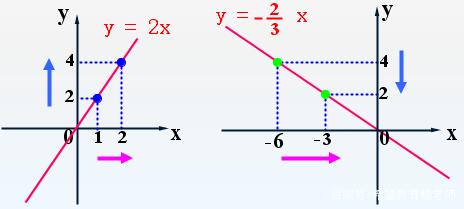
图4

结论：当k＞0时，图象(除原点外)在第一、三象限，x增大时，y的值也增大；y随x的增大而增大；

当k＜0时，图象(除原点外)在二、四象限，x增大时，y的值反而减小；y随x的增大而减小。

例5画出函数y=2x与y=1/2x的图像（图5）以及函数y=-2x与y=-1/2x的图像（图6）。

这两个正比例函数的k不一样，大家观察一下k的值对图像有什么影响？

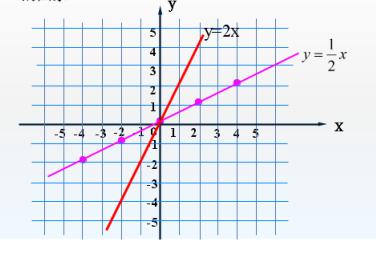
图5

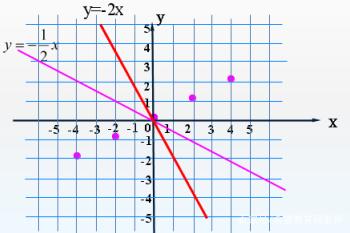
图6

结论：由图5可知，k的值越大函数图像越陡！K代表一次函数的斜率，即倾斜程度。

由图6可知，-2小却更陡，说明k的绝对值越大，函数图像越陡！

第三正比例函数图像的特征及性质

由以上例题可知，正比例函数图像的特征及性质如下：

（1）一般地，正比例函数y=kx（k是常数，k≠0）的图象是一条经过原点的直线；

（2）当k ＞0时，直线y=kx经过第一、三象限，从左向右上升，即随着x的增大y也增大；

（3）当k <0时，直线y=kx经过第二、四象限，从左向右下降，即随着x的增大y而减小：

（4）K代表一次函数的斜率，即倾斜程度。k的绝对值越大，函数图像越陡！

（5）我们称正比例函数y=kx(k≠0)为直线y=kx.