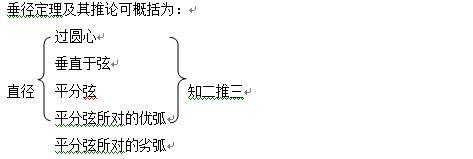
一、垂径定理及其推论

垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧。

推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。

（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧。

（3）平分弦所对的一条弧的直径垂直平分弦，并且平分弦所对的另一条弧。

推论2：圆的两条平行弦所夹的弧相等。

题型巩固

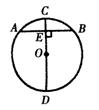
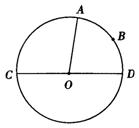
1.如图，CD为⊙O的直径，AB⊥CD于E，DE=8cm，CE=2cm，则AB=______cm．

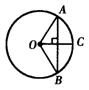
2．如图，⊙O的半径OC为6cm，弦AB垂直平分OC，则AB=______cm，∠AOB=______．

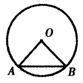
3．如图，AB为⊙O的弦，∠AOB=90°，AB=a，则OA=______，O点到AB的距离=______．

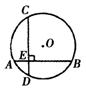
4．如图，⊙O的弦AB垂直于CD，E为垂足，AE=3，BE=7，且AB=CD，则圆心O到CD的距离是______．

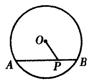
5．如图，P为⊙O的弦AB上的点，PA=6，PB=2，⊙O的半径为5，则OP=______．

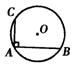
6．如图，⊙O的弦AB垂直于AC，AB=6cm，AC=4cm，则⊙O的半径等于______cm．

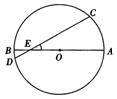
7．已知：如图，AB是⊙O的直径，弦CD交AB于E点，BE=1，AE=5，∠AEC=30°，求CD的长．

8．已知：⊙O的半径为25cm，弦AB=40cm，弦CD=48cm，AB∥CD．

求这两条平行弦AB，CD之间的距离．

9．已知：如图，A，B是半圆O上的两点，CD是⊙O的直径，∠AOD=80°，B是弧AD的中点．

(1)在CD上求作一点P，使得AP＋PB最短；

(2)若CD=4cm，求AP＋PB的最小值．

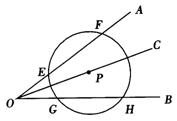
10.已知：如图，P是∠AOB的角平分线OC上的一点，⊙P与OA相交于E，F点，与OB相交于G，H点，试确定线段EF与GH之间的大小关系，并证明你的结论．

二、圆心角、圆周角

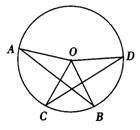
1.已知：如图，A、B、C、D在⊙O上，AB=CD．求证：∠AOC=∠DOB．

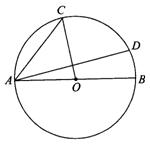
2．已知：如图，AB为⊙O的直径，C，D为⊙O上的两点，且C为弧AD中点，若∠BAD=20°，求∠ACO的度数．

3．如图，若五边形ABCDE是⊙O的内接正五边形，则∠BOC=______，∠ABE=______，∠ADC=______，∠ABC=______．

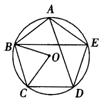
4．如图，ΔABC是⊙O的内接正三角形，若P是弧AB上一点，则∠BPC=______；若M是弧BC上一点，则∠BMC=______．

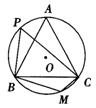
5．如图，弦AB，CD相交于E点，若∠BAC=27°，∠BEC=64°，则∠AOD等于( )．

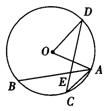
6．如图，△ABC内接于⊙O，∠A=50°，∠ABC=60°，BD是⊙O的直径，BD交AC于点E，连结DC，则∠AEB等于( )．

A．70° B．90° C．110° D．120°

三、综合、运用、诊断

1．已知：如图，△ABC内接于⊙O，BC=12cm，∠A=60°．求⊙O的直径．

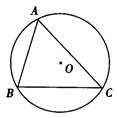
2．已知：如图，AB是⊙O的直径，弦CD⊥AB于E，∠ACD=30°，AE=2cm．求DB长．

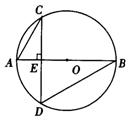
3．已知：如图，△ABC内接于圆，AD⊥BC于D，弦BH⊥AC于E，交AD于F．求证：FE=EH．

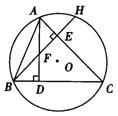
4．已知：如图，⊙O的直径AE=10cm，∠B=∠EAC．求AC的长．

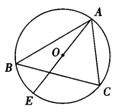
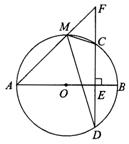
5．已知：如图，AB是⊙O的直径，CD为弦，且AB⊥CD于E，F为DC延长线上一点，连结AF交⊙O于M．求证：∠AMD=∠FMC．