掌握这些几何辅助线技巧，初中数学怎么考都不怕

由角平分线想到的辅助线

1.截取构全等

如图，AB//CD，BE平分∠ABC，CE平分∠BCD，点E在AD上，求证：BC=AB+CD。

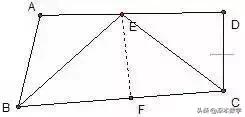
分析：在此题中可在长线段BC上截取BF=AB，再证明CF=CD，从而达到证明的目的。这里面用到了角平分线来构造全等三角形。另外一个全等自已证明。此题的证明也可以延长BE与CD的延长线交于一点来证明。

2.角分线上点向两边作垂线构全等

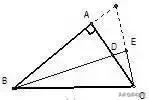
如图，已知AB>AD， ∠BAC=∠FAC，CD=BC。求证：∠ADC+∠B=180°。

分析：可由C向∠BAD的两边作垂线。近而证∠ADC与∠B之和为平角。

3.三线合一构造等腰三角形

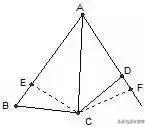
如图，AB=AC，∠BAC=90° ，BD为∠ABC的平分线，CE⊥BE。求证：BD=2CE。

分析：延长此垂线与另外一边相交，得到等腰三角形，随后全等。

4.角平分线+平行线

如图，AB>AC, ∠1=∠2，求证：AB－AC>BD－CD。

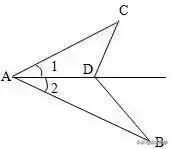
分析：在AB上截取AE=AC，通过全等和组成三角形的三边关系可证。

由线段和差想到的辅助线

1.截长补短法

AC平分∠BAD，CE⊥AB，且∠B+∠D=180°，求证：AE=AD+BE。

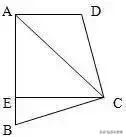
分析：过C点作AD垂线，得到全等即可。

由中点想到的辅助线

1.中线把三角形面积等分

如图，ΔABC中，AD是中线，延长AD到E，使DE=AD，DF是ΔDCE的中线。已知ΔABC的面积为2，求ΔCDF的面积。

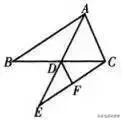
分析：利用中线平分三角形的面积求解。

2.中点联中点得中位线

如图，在四边形ABCD中，AB=CD，E、F分别是BC、AD的中点，BA、CD的延长线分别交EF的延长线于点G、H。求证：∠BGE=∠CHE。

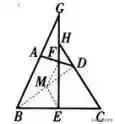
分析：取BD的中点M，连接ME、MF，通过中位线得平行传递角度。

3.倍长中线

如图，已知ΔABC中，AB=5，AC=3，连BC上的中线AD=2，求BC的长。

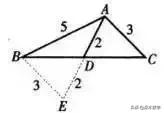
分析：倍长中线得到全等易得。

4.RTΔ斜边中线

如图，已知梯形ABCD中，AB//DC，AC⊥BC，AD⊥BD，求证：AC=BD。

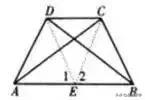
分析：取AB的中点E，得RTΔ斜边中线，得到等量关系。

由全等三角形想到的辅助线

1.倍长过中点得线段

已知，如图△ABC中，AB=5，AC=3，求中线AD的取值范围。

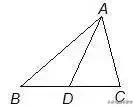
分析：利用倍长中线做。

2.截长补短

如图，在四边形ABCD中，BC＞BA,AD＝CD，BD平分∠ABC，求证：∠A+∠C=180°。

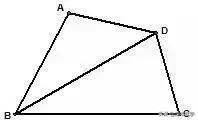
分析：在BC上截取BE=AB，通过全等求证。

3.平移变换

如图，在△ABC的边上取两点D、E，且BD=CE，求证：AB+AC>AD+AE。

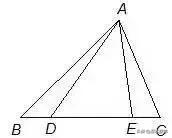
分析：将△ACE平移使EC与BD重合。

4.旋转

正方形ABCD中，E为BC上的一点，F为CD上的一点，BE+DF=EF，求∠EAF的度数。

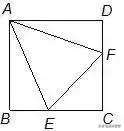
分析：将△ADF旋转使AD与AB重合。全等得证。

由梯形想到的辅助线

1.平移一腰

如图所示，在直角梯形ABCD中，∠A＝90°，AB∥DC，AD＝15，AB＝16，BC＝17. 求CD的长。

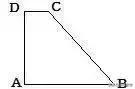
分析：利用平移一腰把梯形分割成三角形和平行四边形。

2.平移两腰

如图，在梯形ABCD中，AD//BC，∠B＋∠C=90°，AD=1，BC=3，E、F分别是AD、BC的中点，连接EF，求EF的长。

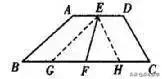
分析：利用平移两腰把梯形底角放在一个三角形内。

3.平移对角线

已知：梯形ABCD中，AD//BC，AD=1，BC=4，BD=3，AC=4，求梯形ABCD的面积。

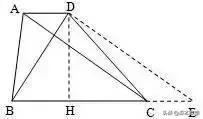
分析：通过平移梯形一对角线构造直角三角形求解。

4.作双高

在梯形ABCD中，AD为上底，AB>CD，求证：BD>AC。

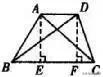
分析：作梯形双高利用勾股定理和三角形三边的关系可得。

5.作中位线

（1）如图，在梯形ABCD中，AD//BC，E、F分别是BD、AC的中点，求证：EF//AD。

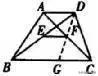
分析：连DF并延长，利用全等即得中位线。

（2）在梯形ABCD中，AD∥BC， ∠BAD=90°，E是DC上的中点，连接AE和BE，求证：∠AEB=2∠CBE。

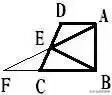
分析：在梯形中出现一腰上的中点时，过这点构造出两个全等的三角形达到解题的目的。