活用等腰三角形“三线合一”巧解题

我们知道，等腰三角形顶角的角平分线、底边上的高、底边上的中线互相重合，（简称“三线合一”），它们所在的直线是等腰三角形的对称轴。等腰三角形“顶角角平分线、底边上的高、底边上的中线”只要知道其中“一线”，就可以说明是其他两线。运用等腰三角形“三线合一”的性质说明角相等、线段相等或垂直关系，可简化解题过程。下面我们将举例说明。

技巧一：利用“三线合一”求角

例1：如图，已知房屋的顶角∠BAC＝100°，过屋顶A的立柱AD⊥BC，屋椽AB＝AC，求顶架上∠B、∠C、∠BAD、∠CAD的度数．

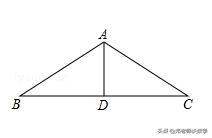
例1图

【分析】先根据等腰三角形的性质得出∠B＝∠C，再由三角形内角和定理即可求出∠B的度数，根据等腰三角形三线合一的性质即可求出∠BAD的度数．

【解答】解：∵△ABC中，AB＝AC，∠BAC＝100°，

∴∠B＝∠C＝40°；

∵AB＝AC，AD⊥BC，∠BAC＝100°，

∴AD平分∠BAC，

∴∠BAD＝∠CAD＝50°．

【点评】本题考查的是等腰三角形的性质及三角形的内角和定理，熟记等腰三角形的性质﹣三线合一是解题的关键．

技巧二：利用“三线合一”求线段

例2：如图，在△ABC中，AB＝AC，AD＝DB＝BC，DE⊥AB于点E，若CD＝4，且△BDC的周长为24，求AE的长．

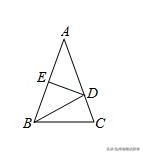
例2图

【分析】由AD＝DB＝BC，CD＝4，且△BDC的周长为24知，AD＝DB＝BC＝10，得AB＝AC＝14，由AD＝DB，DE⊥AB，利用等腰三角形的性质得AE＝BE＝AB＝7．

【解答】解：∵AD＝DB＝BC，CD＝4，且△BDC的周长为24，

∴AD＝DB＝BC＝10，

∴AC＝14，

∵AB＝AC，

∴AB＝14，

∵AD＝DB，DE⊥AB，

∴AE＝BE＝7．

【点评】本题主要考查考了等腰三角形的性质，掌握等腰三角形“三线合一”是解答此题的关键．

技巧三：利用“三线合一”说明线段（或角）相等

例3：已知，在△ABC中，∠A＝90°，AB＝AC，D为BC的中点，E，F分别是AB，AC上的点，且BE＝AF．请你判断△DEF形状，并说明理由；

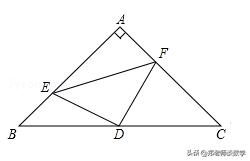
例3图

【分析】连接AD，构造全等三角形：△BED和△AFD．AD是等腰直角三角形ABC底边上的中线，所以有∠CAD＝∠BAD＝45°，AD＝BD＝CD，而∠B＝∠C＝45°，所以∠B＝∠DAF，再加上BE＝AF，AD＝BD，可证出：△BED≌△AFD，从而得出DE＝DF，∠BDE＝∠ADF，从而得出∠EDF＝90°，即△DEF是等腰直角三角形；

【解答】解：△DEF是等腰直角三角形．

如图，连接AD，

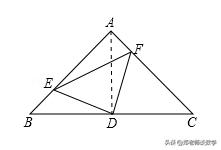
∵AB＝AC，∠BAC＝90°，D为BC中点，

∴AD＝BD＝CD，且AD平分∠BAC，

∴∠BAD＝∠CAD＝45°，

在△BDE和△ADF中，

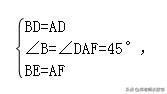
∴△BDE≌△ADF（SAS），

∴DE＝DF，∠BDE＝∠ADF，

∵∠BDE+∠ADE＝90°，

∴∠ADF+∠ADE＝90°，即∠EDF＝90°，

∴△EDF为等腰直角三角形．

【点评】此题主要考查了等腰三角形的性质，全等三角形的判定与性质，关键是画出辅助线，构造全等三角形，利用全等三角形的对应边相等，对应角相等进行推算．

技巧四：利用“三线合一”说明垂直

例4：如图，△ABC中，AC＝2AB，AD平分∠BAC交BC于D，E是AD上一点，且EA＝EC，求证：EB⊥AB．

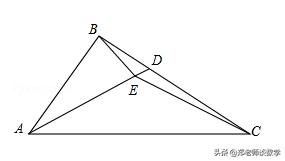
例4图

【分析】作EF⊥AC于F，再根据等腰三角形的性质可得AF＝AC的一半，再证明△ABE≌△AFE可得∠ABE＝∠AFE＝90°．

【解答】证明：作EF⊥AC于F，

∵EA＝EC，

∴AF＝FC，

∵AC＝2AB，

∴AF＝AB，

∵AD平分∠BAC交BC于D，

∴∠BAD＝∠CAD，

在△BAE和△FAE中，

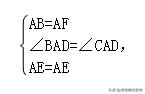
∴△ABE≌△AFE（SAS），

∴∠ABE＝∠AFE＝90°．

∴EB⊥AB．

技巧五：利用“三线合一”说明线段的倍数关系

例5：如图，已知在Rt△ABC中，∠A＝90°，BD是∠ABC的平分线，DE是BC的垂直平分线．试说明BC＝2AB．

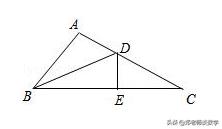
例5图

【分析】DE垂直平分BC，则有BC＝2BE，只要证明BE＝AB即可，由BD是∠B的平分线，∠DAB＝∠DEB＝90°，BD＝BD，可证△ABD≌△EBD，从而有BE＝AB．

【解答】证明：∵DE是BC的垂直平分线，

∴BE＝EC，DE⊥BC，

∵∠A＝90°，

∴DA⊥AB．

又∵BD是∠ABC的平分线，

∴DA＝DE，

又∵BD＝BD，

∴△ABD≌△EBD，

∴AB＝BE，

∴BC＝2AB．

【点评】本题考查了垂直平分线的性质，角平分线的性质，以及全等三角形的判定及其性质的运用．