初中数学，“将军饮马”的七大模型

cc518学习网精品学习资料总目录

让我们先来了解“将军饮马”这个故事。

古希腊亚里山大里亚城有一位久负盛名的学者，名叫海伦。

有一天，有位将军不远千里专程前来向海伦求教一个百思不得其解的问题：如图，将军A从出发到河边饮马，然后再到B地军营视察，显然有许多走法．问怎样走路线最短呢？精通数理的海伦稍加思索，便作了完善的回答．这个问题后来被人们称作“将军饮马”问题．

下面我们来看看数学家是怎样解决的．海伦发现这是一个求折线和最短的数学问题．

根据公理：连接两点的所有线中，线段最短．

若A、B在河流的异侧，直接连接AB，AB与l的交点即为所求．

若A、B在河流的同侧，根据两点间线段最短，那么显然要把折线变成直线再解．

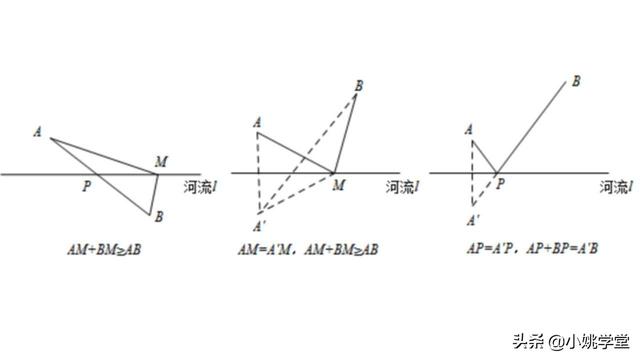
将军饮海伦解决本问题时，是利用作对称点把折线问题转化成直线

现在人们把凡是用对称点来实现解题的思想方法叫对称原理，即轴对称思想

轴对称的两个图形有如下性质：

①关于某条直线对称的两个图形是全等形；

②对称轴是任何一对对应点所连线的垂直平分线；

③两个图形关于某条直线对称，如果他们的对应线段或延长线相交，那么交点在对称轴上．

将军饮马的数学问题，考察的知识点：“两点之间线段最短”，“垂线段最短”，“点关于线对称”，“线段的平移”。

解题总思路：找点关于线的对称点实现“折”转“直”，近两年出现“三折线”转“直”等变式问题考查。共有七大模型：

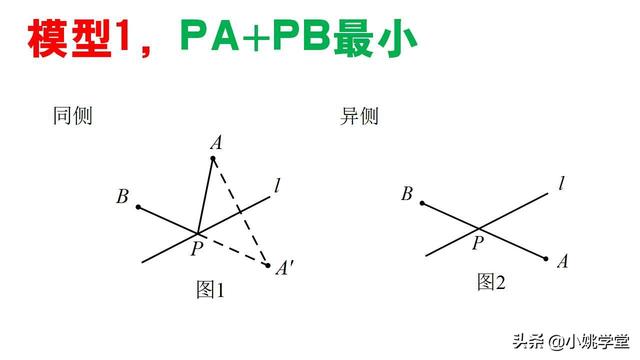
模型1，PA+PB最小

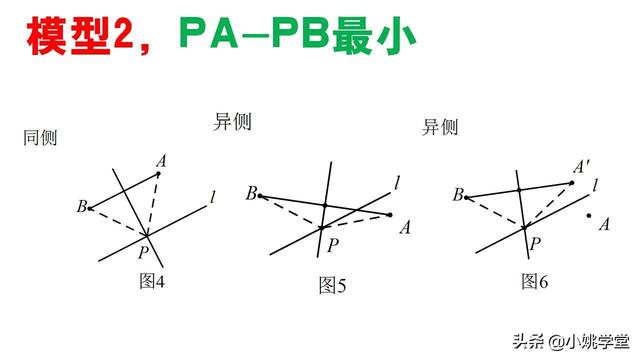
模型2，PA-PB最小

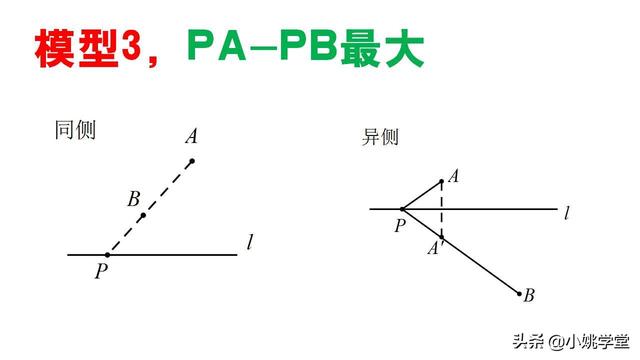
模型3，PA-PB最大

【变形】异侧时，也可以问：在直线l上是否存在一点P使得直线l为∠APB的角平分线

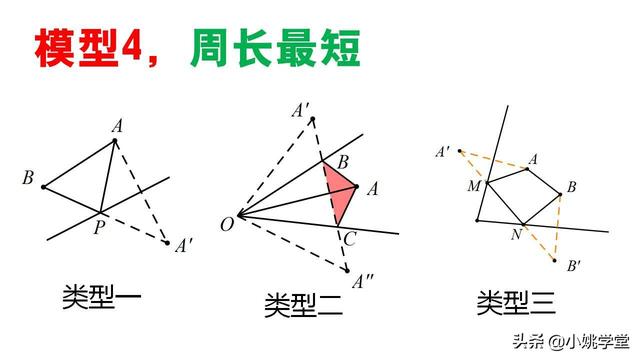
模型4，周长最短

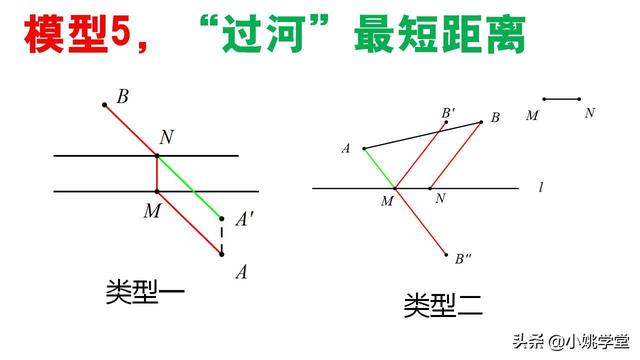
模型5，“过河”最短距离

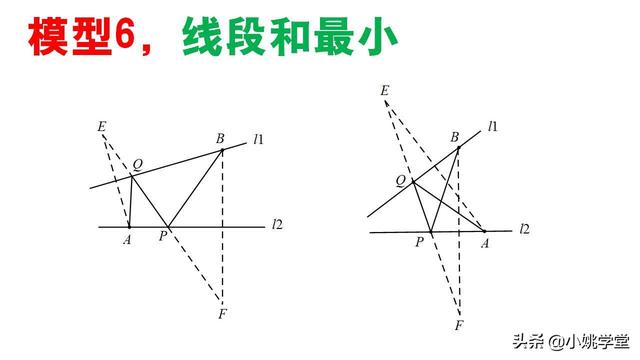
模型6，线段和最小

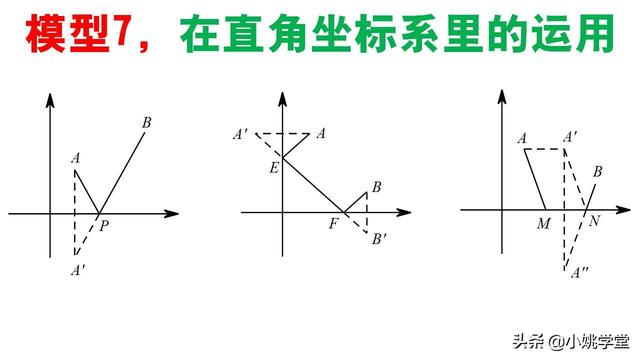
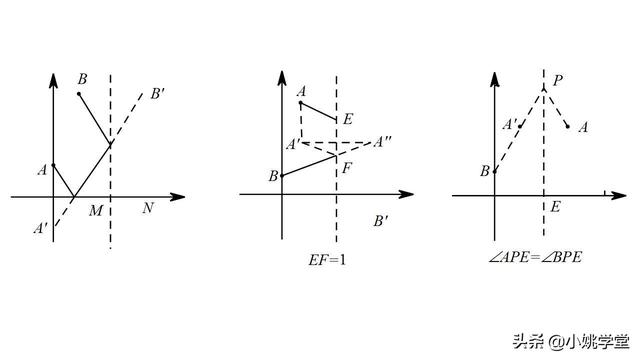
模型7，在直角坐标系的运用

题目巩固

1.如图，直线 l 和 l 的异侧两点 A、B，在直线 l 上求作一点 P，使 PA+PB 最小。

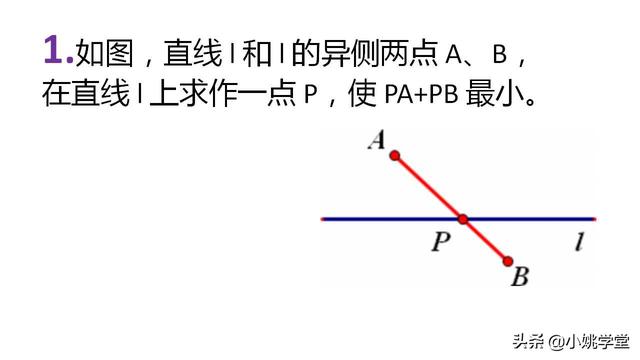
2.如图，直线 l 和 l 的同侧两点 A、B，在直线 l 上求作一点 P，使 PA+PB 最小。

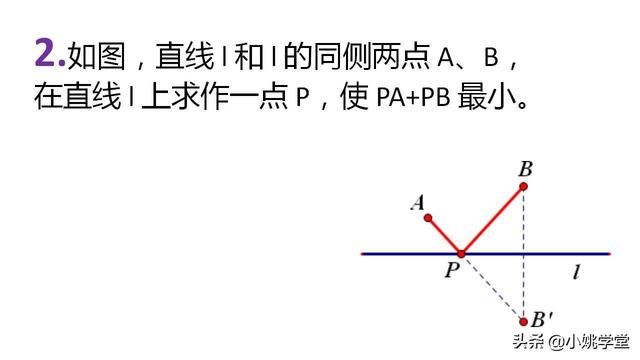
3.如图，点 P 是∠MON 内的一点，分别在 OM，ON 上作点 A，B。使△PAB 的周长最小

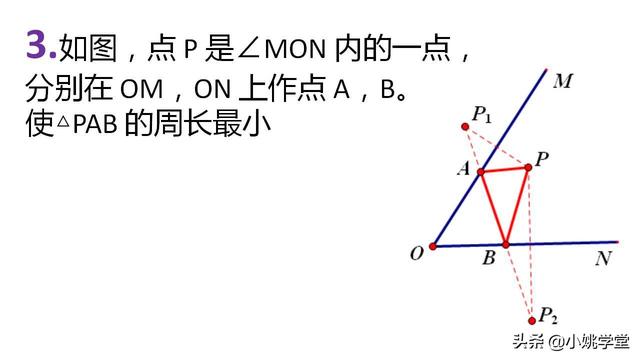
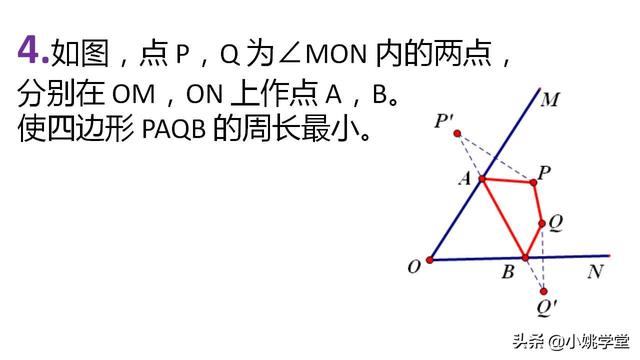
4.如图，点 P，Q 为∠MON 内的两点，分别在 OM，ON 上作点 A，B。使四边形 PAQB 的周长最小。

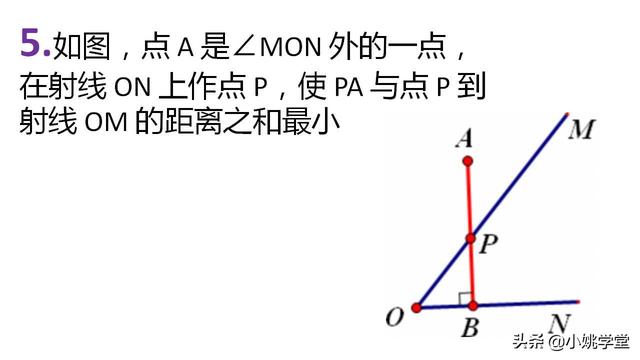
5.如图，点 A 是∠MON 外的一点，在射线 ON 上作点 P，使 PA 与点 P 到射线 OM 的距离之和最小

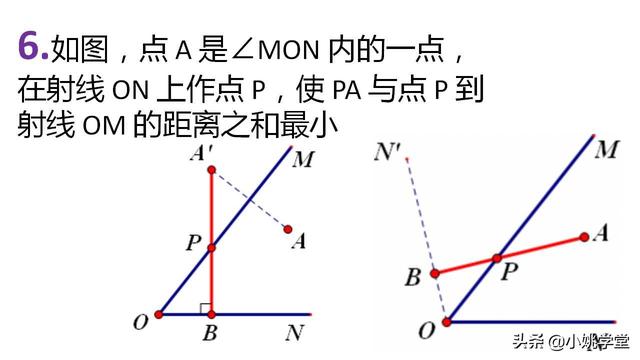
6.如图，点 A 是∠MON 内的一点，在射线 ON 上作点 P，使 PA 与点 P 到射线 OM 的距离之和最小

当已知条件出现了等腰三角形、角平分线、高，或者求几条折线段的最小值等情况，通常考虑作轴对称变换，以“补齐”图形，集中条件。

所有的轴对称图形（角、线、等腰三角形、等边三角形、菱形、矩形、正方形、等腰梯形、圆、坐标轴），都可以考察“将军饮马”问题。